Для создания математических и компьютерных моделей учебного процесса, установления качественных и количественных закономерностей распределения учебной информации необходимо уметь оценивать различные качества педагогических объектов: уровень знаний учеником учебного материала, сложность понятий, формул, тем, задач, информативность рисунков и т.д. [1, 6]. Применение математических методов в дидактике и других гуманитарных областях отвечает важному принципу научного познания: исследуемый объект (явление) нельзя считать хорошо изученным, пока он не описан с помощью количественных характеристик [2, с. 9]. Анализ, оценка и сравнение учебников, учебных пособий и методик требуют определения каких–то объективных и относительно устойчивых характеристик элементов учебного материала (ЭУМ) [4, 5]. Такими характеристиками ЭУМ являются дидактическая сложность (ДС) и информативность или количество информации (КИ).
При обсуждении проблемы оценки того или иного качества дидактического объекта следует помнить о принципе несовместимости: высокая точность измерений (оценок, предсказаний) несовместима с большой сложностью изучаемой системы [2, с. 10]. Действительно, если объект состоит из большого числа разнородных элементов, связанных между собой разнотипными связями, то построить его модель, точно соответствующую оригиналу, практически невозможно. Л. Заде отмечал, что “для получения существенных выводов о поведении гуманистических систем придется, по-видимому, отказаться от высоких стандартов точности и строгости, которые мы, как правило, ожидаем при математическом анализе четко определенных механистических систем, и относиться более терпимо к иным подходам, которые являются приближенными по своей природе” [2, с. 10]. При увеличении точности измерения той или иной характеристики уменьшается достоверность. Поэтому при анализе сложных систем приходится “жертвовать точностью перед лицом ошеломляющей сложности” [2, с. 10].
Из теории систем [3] следует, что любой рисунок, схема, формула есть совокупность связанных между собой элементов. Для оценки КИ и ДС рисунка его заменяют полным, но предельно кратким описанием и подсчитывают количество и сложность используемых понятий. Другой подход предполагает определение количества и степени абстрактности изображенных на рисунке объектов и связей между ними. Перечислим примеры таких связей: взаимодействие Солнце–Земля, нить соединяющая два тела, причинно–следственные связи, перпендикуляры, опускаемые на координатные оси. Критерием абстрактности объекта (или связи) является невозможность школьника пронаблюдать данный или подобный ему объект (связь) непосредственно, ощутить его с помощью органов чувств. Для оценки ДС рисунка необходимо определить: 1. Число x_1 изображений физических объектов, которые школьник может пронаблюдать, ощутить органами чувств непосредственно. 2. Число x_2 физических связей, которые школьник может пронаблюдать (гальванометр подключен к катушке; микрофон расположен напротив динамика; кислота налита в колбу; в жидкость опущен термометр и т.д.). 3. Число x_3 изображений реально существующих физических объектов, которые школьник не может ощутить органами чувств и вынужден представлять (атом, электрон, хромосома, ЭМ поле). 4. Число связей x_4, которые школьник не может ощутить органами чувств и вынужден представлять (химические связи, притяжение электронов к ядру атома, абстрактные связи, изображенные в виде стрелок). 5. Число x_5 математических абстракций (математические формулы и обозначения, геометрические фигуры и тела, вектора, координатные оси, графики). 6. Число x_6 надписей, обозначающих объекты (явления), которые школьник может пронаблюдать (надписи “Солнце”, “бензин”, “клетка”). 7. Число x_7 надписей, обозначающих объекты (явления), которые школьник не может ощутить органами чувств и вынужден представлять (надписи “HNO”, “кварки”, “лейкоциты”).
Рисунок может содержать m условных обозначений реально существующих объектов, которые школьник может ощутить органами чувств. Например, схема электрической цепи состоит из абстрактных элементов, соответствующих реальным объектам, которые школьник может рассмотреть и потрогать. В этом случае x_1 и x_3 необходимо увеличить на m/2 каждый.
Общая информативность I рисунка и количество I_a абстрактной информации (в понятиях) равны: I = x_1 + x_2 + … + x_7, I_a = x_3 + x_4 + x_5 + x_7. Коэффициент абстрактности и доля математической информации находятся по формулам: K_a = I_a / I, K_m = x_5 /I.Дидактическая сложность (ДС) рисунка равна его информативности с учетом сложности составляющих элементов; она определяется взвешенной суммой S = (I – I_a) + a*I_a, где a – весовой коэффициент, превышающий 1. Так как переход на другой качественный уровень связан с увеличением количества соответствующего качества в e = 2,72… раза, то будем считать, что a = 2,72. На рис. 1 представлены четыре рисунка из школьных учебников физики и химии; рядом приводятся вектор характеристик (x_1, x_2, …, x_7), информативность (КИ) I, коэффициенты K_a и K_m и дидактическая сложность S. Полученные значения позволяют сравнить рисунки по их дидактической сложности. Например, видно, что рис. 1.1 примерно в два раза информативнее рис. 1.4, а его ДС в три раза больше, чем у рис. 1.2.
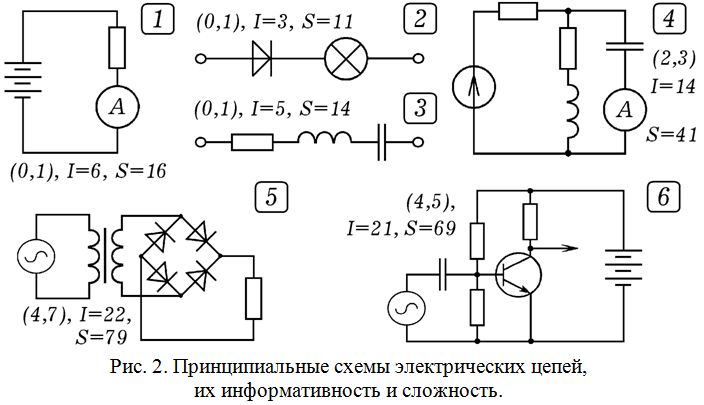
Для оценки КИ и ДС электрической схемы следует составить ее словесное описание. Например (рис. 2.4): “Цепь состоит из источника переменного напряжения, имеет два узла и три ветви. Ветвь 1: соединенные последовательно генератор и резистор. Ветвь 2: соединенные последовательно резистор и катушка индуктивности. Ветвь 3: соединенные последовательно конденсатор и амперметр”. После этого необходимо подсчитать все понятия и просуммировать их сложности.
Возможен другой подход, состоящий в использовании компьютерной программы, которая анализирует файл, содержащий список всех приборов, входящих в электрическую цепь, и задает вопросы о количестве узлов и ветвей в цепи. Программа работает с словарем–тезаурусом; это текстовый файл shema.txt, в котором перечислены названия приборов (резистор, конденсатор, операционный усилитель и т.д.) и для каждого прибора указана сложность (формат: “название прибора”, s_i). Вот фрагмент этого файла: “… резистор 3, конденсатор 3, катушка 1, индуктивности 2, вольтметр 2, амперметр 2, ваттметр 3, диод 4, транзистор 5, …”. Задача эксперта состоит в том, чтобы создать текстовый файл, соответствующий рассматриваемой электрической цепи, определить число узлов x_1, число ветвей x_2 и, запустив программу, ввести эти данные. Программа выдает: 1) количество информации (КИ) в схеме, равное сумме всех понятий N, используемых в словесном описании: I = N; 2) ДС схемы S = s_1 + s_2 + … + s_N + 3x_1 + 5x_2, где s_i – сложность i–ого понятия по шкале 1 – 2 – 3 – 4 – 5.
На рис. 2 приведены получающиеся оценки КИ I и ДС S шести электрических схем. При оценке схемы транзисторного усилителя (рис. 2.6) текстовый файл shema.txt содержит перечень: “батарея гальванических элементов, источник переменного напряжения, конденсатор, резистор, резистор, резистор, транзистор”; x_1 = 4, x_2 = 5. Каждой схеме соответствуют вектор (x_1, x_2), количество информации (КИ) I и дидактическая сложность (ДС) S. Коэффициенты K_a = 0,5, K_m = 0.
Аналогичным образом может быть оценена сложность химической формулы вещества или химической реакции. Для анализа химической формулы HSO создается текстовый файл form.txt, в который вводят H_2SO_4, что означает: “молекула содержит два атома водорода, атом серы, 4 атома кислорода”. Для анализа химической формулы CuSO + 2NaOH = Cu(OH) +2NHCl в текстовый файл form.txt вводят: CuSO_4+2NaOH = Cu(OH)_2+2NH_4Cl. Данную формулу можно заменить словесным описанием типа: “Одна молекула, состоящая из атома меди, атома серы и четырех атомов кислорода, соединяется с двумя молекулами, состоящими из атома натрия, атома кислорода и атома водорода. В результате получается …”. КИ и ДС могут быть определены путем подсчета терминов и учета их сложности.
Используемая компьютерная программа анализирует текстовый файл с записями химических формул, подсчитывает количество различных символов, учитывает их сложность и задает следующие вопросы: 1) Сколько различных молекул x_1 в записи (без учета коэффициентов)? 2) Сколько изображено связей x_2? Второй вопрос позволяет учесть изображения химических связей в структурных формулах (рис. 3). При этом используется словарь, в котором перечислены химические элементы, цифры и другие символы с указанием их сложности: “… Cu 5, Br 6, H 6, B 6, C 5, N 6, …”. Символ C означает понятие “атом углерода”, его сложность 5. После запуска компьютерная программа выдает КИ I, равное числу используемых понятий, и ДС S. Если химическая формула содержит бензольные кольца, то в файле form.txt необходимо указать “бензольное_кольцо”; его сложность считается равной 18. На рис. 3 представлены примеры формул химических реакций, соответствующие им описания (в кавычках), значения (x_1, x_2), а также получающиеся значения КИ и ДС.
В статье рассматриваются методы оценки информативности и дидактической сложности учебных рисунков и химических реакций, основывающиеся на разделении этих объектов на отдельные элементы и учете их сложности. Приводятся многочисленные примеры использования данного метода. Полученные результаты могут быть применены для оценки информативности и дидактической сложности учебников.
Библиографический список
- Беспалько, В.П. Теория учебника: Дидактический аспект. – М.: Педагогика, 1988. – 160 с.
- Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М: Мир, 1976. – 165 с.
- Лаврушина, Е.Г., Слугина, Н.Л. Теория систем и системный анализ: Учебное пособие. – Владивосток: Издательство ВГУЭС, 2007. – 171 с.
- Майер, Р.В. Об оценке сложности элементов учебного материала школьного курса физики // Гуманитарные научные исследования. – 2015. – N 12 [Электронный ресурс]. URL: http://human.snauka.ru/2015/12/13535
- Майер, Р.В. Оценка дидактической сложности физических понятий методом парных сравнений // Мир науки. Научный интернет–журнал [Электронный ресурс]. – 2014, Выпуск 3. – 8 с.
- Микк, Я.А. Оптимизация сложности учебного текста: В помощь авторам и редакторам. – М.: Просвещение, 1981. – 119 с.