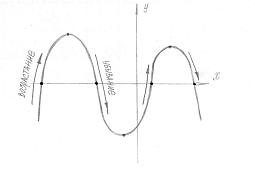
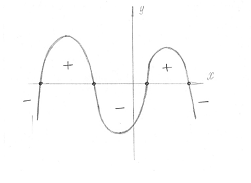
Учащиеся 10-11 классов приступают к изучению курса «Алгебры и начал анализа». Начала анализа представлены, прежде всего, изучением производной и ее применения. Как показывает практика преподавания и результаты ЕГЭ, материал является сложным для учащихся. Однако тесты ЕГЭ содержат два задания (В8 и В14), которые требую знания и применения производной. Поэтому остается актуальным совершенствование методики преподавания производной и ее применения.
Анализируя существующие методики в современной практике преподавания математики, приходим к выводу, что методика обучения производной заключается в изучении теоретических основ (не всегда с выводом формул и не всегда изучению производной предшествует изучение теории пределов), заучиванию формул, решению задач по образцу. Однако, задачи содержащие график функции или график производной функции, требуют владения материалом, то есть не просто знать правило, но и суметь увидеть его, применить в заданной ситуации. Причем, учащиеся должны применять именно ту теорию, которая необходима для решения данной задачи. В этом и состоит трудность, которую испытывают учащиеся. Для того чтобы эту трудность устранить, мы предположили, что в традиционную методику обучения учащихся необходимо внести следующую процедуру: при обучении применению производной к исследованию функции следует рассматривать задачу с двумя условиями и одним требованием.
Рассмотрим методику обучения учащихся нахождению промежутков возрастания и убывания непрерывной функции с учетом нашего предположения.
Сначала учащиеся определяют на координатной оси нули функции, которые рассматриваются как на графике самой функции, так и на графике ее производной; необходимое условие – добиваемся четкого осознания понятия нули функции, критическая точка. Затем изучаются признаки возрастания и убывания функции, основанные на производной, где так же решаются задачи с использованием не только графика функции, но и графика ее производной. После чего исследуют функцию с помощью производной. Таким образом, ключевым в описываемой методике является совместное рассмотрение графиков функции и графиков производной функции, чтобы у учащихся формировалось четкое представление о том, какие теоремы и какие методы следует применять в каждом из случаев.
Покажем на примере серию задач, направленных на формирование умения исследования функций по графикам самой функции и по графику ее производной.
Задача 1. На рисунке (Рис. 1) изображен график функции f(x), определенной на отрезке [−4; 6]. Определите по графику промежутки убывания и возрастания.
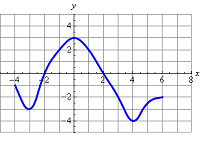
Рис. 1
Решение.
-
Отметим границы графика [−4; 6], а также нули производной x=−2 и x=2.
-
На промежутке (−4; −2) для любых x1 и x2, таких, что x1 > x2 выполнимо неравенство f(x1) < f (x2), следовательно, функция на данном интервале убывает. На промежутке (−2; 0) для любых x1 и x2, таких, что x1 > x2 выполнимо неравенство f (x1) > f (x2) следовательно, функция на данном интервале возрастает. Аналогично, на промежутке (0; 4) функция будет убывать, а на промежутке (4; 6) возрастать.
Ответ:
Интервалы убывания функции: (−4; −2) U (0;4). Интервалы возрастания функции: (−2; 0) U (4; 6).
Задача 2. На рисунке (Рис. 2) изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Определите по графику промежутки убывания и возрастания.
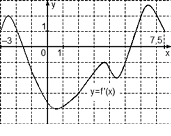
Рис. 2
Решение.
-
Отметим границы графика [−3; 7,5], а также нули производной: x=−1,5 и x=5,3. Затем отметим знаки производной. Имеем:

Рис. 3
-
Поскольку на интервале (−1,5; 5,3) производная отрицательна, это и есть интервал убывания функции. А интервалами возрастания будут являться: (−3; −1.5) и (5,3; 7,5).
Ответ: Интервал убывания функции: (−1,5; 5,3). Интервалы возрастания функции: (−3; −1.5) и (5,3; 7,5).
Итак, нахождение промежутков возрастания и убывания зависит от того, какой график нам дан в условии: график функции или график её производной. Приведем сравнительную таблицу (Таблица 1) по нахождению промежутков возрастания и убывания по графику.
Таблица 1
|
Задача. Дан график, по графику определить промежутки возрастания и убывания. |
|
|
Если дан график функции y=f(x).
|
Если дан график производной функции y=f `(x).
|
|
|
Нами было проведено экспериментальное обучение учащихся в школах г.Волгограда с учетом нашего предположения. Мы получили положительные результаты.
Таким образом, сравнительный анализ и совместное рассмотрение задач на нахождение промежутков возрастания и убывания в задачах, содержащих в условии график функции или её производной, способствует более глубокому усвоению знаний и владению материалом не только на теоретическом уровне, но и в практическом применении.
Библиографический список
- Лященко, Е.И. Изучение функций в курсе математики восьмилетней школы / Е.И. Лященко – Мн.: «Нар. асвета», 1970. – 176 с.
- Методика и технология обучения математике. Курс лекций: пособие для вузов / под. Научн. Ред. Н.Л. Стефановой, Н.С., Н.С. Подходовой. – М: Дрофа, 2005. – 416 с..
- Мордкович, А.Г. Алгебра и начала анализа. 10кл.: В двух частях. Ч. 1: Учеб. для общеобразоват. учреждений (профильный уровень) / А. Г. Модкович, П. В. Семенов. – М.: Мнемозина, 2005. – 408 с.: ил.