Деятельность мышления взрослого человека проявляется главным образом при решении задач, которые постоянно выдвигает перед людьми жизнь. Решение задач всегда даёт человеку что-то новое, новые знания. Обучение подрастающего поколения основам наук стремится именно к такой организации познавательной деятельности учащихся. Именно поэтому общепризнанна значимость использования в обучении прикладных задач, задач с практическим содержанием.
Задачи оптимизации – это один из ярких примеров прикладных задач. Их решение предполагает выбор наилучшего варианта из множества возможных. Если критерий выбора известен и вариантов немного, то решение может быть найдено путем перебора и сравнения всех вариантов. Однако часто бывает так, что число возможных вариантов настолько велико, что полный перебор практически невозможен. В таких случаях приходится формулировать задачу на языке математики и применять специальные методы поиска оптимального решения.
Значительно упрощает решение задач оптимизации использование компьютера и специальных программных средств. В данной статье рассмотрим основы решения задач оптимизации с помощью электронных таблиц LibreOffice Calc.
В электронных таблицах Calc для этого предусмотрены два средства:
1) подбор параметра (определяет значение одной входной ячейки, которое требуется для получения желаемого результата в зависимой ячейке);
2) решатель (определяет значения в нескольких входных ячейках, которые требуются для получения желаемого результата).
Изучать технологию решения задач оптимизации в электронных таблицах на начальных этапах нужно со средства «Подбор параметра». Это обоснованно тем, что подбор параметра используется для решения более простых задач (осуществляется подбор значения одной ячейки, а не нескольких). С целью иллюстрации использования данного средства приведем примеры решения задач.
Пример 1.
Вы хотите положить деньги в банк под 5,5% и получить ровно 30000 руб. по истечении года. Определите сумму вклада.
Решение
1. Оформим таблицу с исходными данными и введем указанную формулу (рис. 1).
Рисунок 1 – Исходные данные
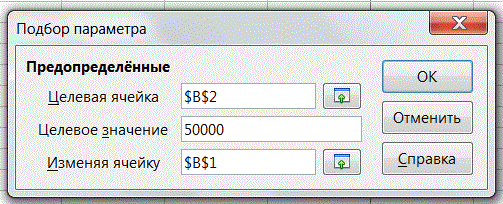
2. Активизируем ячейку В3 и выполним команду Сервис >Подбор параметра. В открывшемся диалоговом окне укажем значение необходимой конечной суммы и ссылку на ячейку с искомым значением вклада (рис. 2).
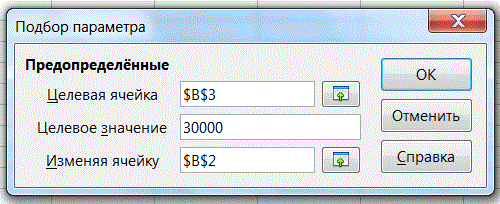Рисунок 2 – Диалоговое окно №1 средства «Подбор параметра»
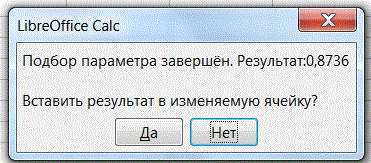
Нажмём кнопку ОК. Средство «Подбор параметра» найдет решение и сообщит об этом (рис. 3).
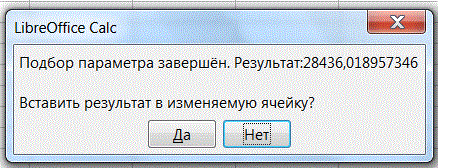Рисунок 3 – Диалоговое окно №2 средства «Подбор параметра»
Нажмём кнопку Да и убедимся, что искомое значение будет помещено в ячейке В2 (рис. 4).
Рисунок 4 – Исходные данные и искомый результат
Решение приведенной задачи, на первый взгляд, кажется довольно простым. Действительно, оно предельно лаконично и его реализация занимает не более 5 мин. Однако самостоятельное решение подобных задач учащимися, особенно на начальном этапе, сопровождается трудностями. Эти трудности содержательного характера: проблема не в технологии использования средства «Подбор параметра», а в анализе исходных данных и их взаимосвязи с искомым результатом.
Самостоятельное решение задач оптимизации средствами электронных таблиц требует осуществления таких мыслительных операций, как анализ и синтез, сравнение, абстрагирование и конкретизация.
Опишем поиск решения следующей задачи оптимизации.
Пример 2
Определите годовую ставку банка по займу величиной 50000 руб., сделанному на 3 года, если ежемесячные платежи составляют 1500 руб.
Решение
1. Сравним формулировку данной задачи с вышеприведенной, т.е. определим сходства и различия между ними.
Сходство: обе задачи экономического содержания, в которых рассматривается ситуация взаимодействия физического лица и банка; во второй задаче также как и в первой нужно определить значение одной входной ячейки (годовую ставку по займу);
Различия: рассматриваемые ситуации в приведенных задачах содержательно противоположны – в первой задаче физическое лицо делает вклад в банк с определенным годовым процентом, во второй задаче физическое лицо берет кредит в банке с некоторой годовой ставкой.
Сравнение формулировок задач позволяет сделать вывод о том, что 1) вторая задача также может быть решена с помощью средства «Подбор параметра»; 2) решение второй задачи основано на той же зависимости исходных величин, что и в первой задаче.
2. Проанализируем исходные данные, т.е. выделим из целостной формулировки отдельные величины, которые фигурируют в задаче: годовая ставка (в %), величина займа (в руб.), срок займа (в г.), ежемесячные платежи (в руб.).
Оформим таблицу в Calc с исходными данными (рис. 5).
Рисунок 5 – Исходные данные
3. Определим зависимость между выделенными величинами, попытаемся понять в какой математической формуле они объединяются (т.е. применим мыслительную операцию синтеза). По аналогии с первой задачей зависимость между величинами следующая:
1500·12·3=50000+50000·x·3, где – искомая годовая ставка (в %). (1)
4. Мысленно отвлечемся от содержания наших величин (т.е. применим мыслительную операцию абстрагирования) и подумаем над тем, как будут заполняться поля в диалоговом окне средства «Подбор параметра»:
«Целевая ячейка» – однозначно ячейка со значением годовой ставки (в %), т.е. В1;
«Целевое значение» – число 50000 (величина займа);
«Изменяя ячейку» – ячейка В2, которая содержит формулу для расчета величины займа при известной годовой ставке, срока займа и размера ежемесячных платежей.
5. Формулу для ячейки В2 получим из (1):
1500·12·3=50000(1+x·3);
50000=(1500·12·3)/(1+x·3).
Или с использованием ссылок на ячейки в данной задаче: B2=(B4*12*B3)/(1+B1*B3).
6. Оформим таблицу с исходными данными и введем указанную формулу (рис. 6). Формат ячейки В1 установим «Процентный».
Рисунок 6 – Исходные данные и зависимость между ними
7. Активизируем ячейку В2 и выполним команду Сервис > Подбор параметра. В открывшемся диалоговом окне укажем значение необходимой величины займа и ссылку на ячейку с искомой годовой ставкой (рис. 7).
Рисунок 7 – Диалоговое окно №1 средства «Подбор параметра»
Нажмём кнопку ОК. Средство «Подбор параметра» найдет решение и сообщит об этом (рис. 8).
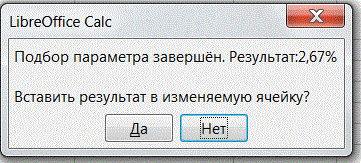Рисунок 8 – Диалоговое окно №2 средства «Подбор параметра»
Нажмём кнопку Да и убедимся, что искомое значение будет помещено в ячейке В1 (рис. 9).
Рисунок 9 – Исходные данные и искомый результат
8. Итак, годовая ставка банка по займу величиной 50000 руб., сделанному на 3 года при ежемесячных платежах в 1500 руб., составит 2,67% (конкретизация формального значения, полученного в ячейке В2).
Замечание
Такой глубокий анализ задачи в примере 2 позволяет найти её решение и без использования средства «Подбор параметра»:
1) найдем общую сумму платежей за 3 года: В6=В4*12*В3;
2) найдем сумму переплаты в год: В7=(В6-В2)/В3;
3) найдем годовую ставку (в %): В8=(В7*100)/В2 (рис. 10).
Рисунок 10 – Решение задачи в примере 2 без использования подбора параметра
Приведем теперь пример задачи не экономического содержания, которую также можно решить с помощью средства «Подбор параметра».
Пример 3
Методом подбора параметра найдите корень уравнения x^3-sin(x)+0,1=0 с точностью до четырех знаков после запятой.
Решение
1. Рассмотрим функцию y(x)=x^3-sin(x)+0,1. И подберем значение переменной x, чтобы значение функции y(x)=0.
Оформим таблицу с исходными данными и введем указанную формулу (рис. 11).
Рисунок 11 – Исходные данные
Формат ячейки B1 установим «Числовой», дробная часть – 4 знака после запятой.
2. Активизируем ячейку В2 и выполним команду Сервис > Подбор параметра. В открывшемся диалоговом окне укажем значение необходимого значения функции и ссылку на ячейку с искомым значением переменной (рис. 12).
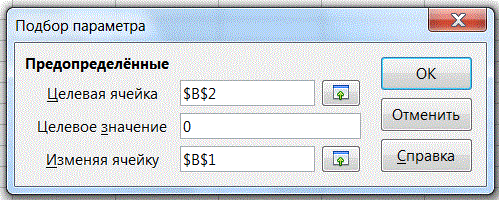Рисунок 12 – Диалоговое окно №1 средства «Подбор параметра»
Нажмём кнопку ОК. Средство «Подбор параметра» найдет решение и сообщит об этом (рис. 13).
Рисунок 13 – Диалоговое окно №2 средства «Подбор параметра»
Нажмём кнопку Да и убедимся, что искомое значение будет помещено в ячейке В2 (рис. 14).
Рисунок 14 – Исходные данные и искомый результат
Замечание
Методом подбора параметра в электронных таблицах можно решать различные уравнения. Данное средство легко и быстро сможет найти как точное значение корня уравнения, так и приближенное.
Однако нужно помнить, что уравнение может иметь несколько корней, а средство «Подбор параметра» укажет только один из них.
Приведенные примеры иллюстрируют многообразие задач оптимизации, которые легко можно решить методом подбора параметра в электронных таблицах. Эти задачи с практическим содержанием, они интересны для исследования, а решение их способствует развитию у учащихся таких мыслительных операций, как анализ, синтез, сравнение, абстрагирование и конкретизация.