В процессе решения задач по программированию можно выделить следующие этапы:
1) параметризация или постановка задачи, предполагающие анализ условия, выделение аргументов и результатов решения;
2) построение математической модели;
3) построение алгоритма;
4) программная реализация алгоритма;
5) отладка программного кода;
6) тестирование программы.
Зачастую студенты пропускают первые три этапа и переходят сразу к написанию программы. Это связано, прежде всего, с тем, первые три этапа наиболее сложные и трудоемкие. Однако, они необходимы, так как без правильного понимания условия задачи, без построения адекватной математической модели и ее реализации в виде алгоритма невозможно создание оптимальной, правильной и эффективной программы, что доказано всем опытом программирования [1]. Неслучайно профессия программиста зачастую называется как «математик-программист». Это отражает сущность профессии, а также тот смысл, который изначально вкладывался в понятие «программирование». Программирование есть не ремесло, а акт творчества, который невозможен без фундаментальных знаний в области математики и информатики [2]. Поэтому умение грамотно построить математическую модель является неотъемлемым профессиональным качеством будущего программиста. В этой связи опишем процесс построения математических моделей при решении задач, относящихся к предметной области вычислительной геометрии.
Вычислительная геометрия – это интересная и сравнительно молодая область компьютерной науки, находящаяся на стыке информатики и геометрии и сочетающая геометрические понятия, идеи и модели с понятиями, идеями и методами разработки алгоритмов и структур данных. Появление компьютеров и последовавшее за этим бурное развитие информатики открыли возможность симбиоза чисто геометрической природы задач на построение с аналитическим подходом к их решению, что, в свою очередь, привело к возможности решения нового класса задач, которыми и занимается вычислительная геометрия. Данные задачи применяются в компьютерной графике и визуализации данных; в робототехнике; в географических информационных системах; в системах автоматизированного проектирования; компьютерной томографии; в дизайне микросхем и других областях науки, техники и производства.
В задачах вычислительной геометрии исходными данными, как правило, являются геометрические объекты (множество точек, набор отрезков, многоугольник), а результатами могут выступать ответы на вопросы о некоторых отношениях между заданными объектами (пересекаются ли заданные отрезки, является ли многоугольник выпуклым); перечисление фактов относительно этих отношений (перечисление всех пар пересекающихся отрезков); построение нового геометрического объекта (наименьшего выпуклого многоугольника, содержащего заданные точки) и т.п.
Характерным представителем класса алгоритмов вычислительной геометрии является задача о пересечении отрезков, которая находит свое применение в решении следующих практических задач:
- в геоинформационных системах (и не только в них) используются разнообразные географические карты. На картах отображается множество объектов: населенные пункты, границы, реки и другие водоемы, овраги и горы, дороги разного типа, мосты, линии электропередач и другие промышленные объекты. Все эти объекты представляются определенными геометрическими образами, многие из которых можно считать так или иначе состоящими из прямолинейных отрезков. Поэтому определение пересечения географических объектов, например, дорог, рек, границ и т. п., сводится к нахождению пересечений множества отрезков;
- в машинной графике требуются методы удаления невидимых линий и поверхностей в трехмерных сценах, когда различные объекты сцены частично перекрывают друг друга. Не имея оптимального алгоритма определения попарных пересечений отрезков из заданного набора, трудно рассчитывать на эффективную реализацию удаления невидимых линий;
- в микроэлектронике возникает необходимость проверки пересечения различных компонентов интегральных схем, состоящих из большого количества элементов (до миллиона и более), что невозможно осуществить без компьютерных методов, в том числе без алгоритмов пересечения геометрических объектов.
Задача о пересечении отрезков на плоскости может быть представлена в одной из следующих формулировок:
Задача № 1: проверить, пересекаются ли заданные прямолинейные отрезки;
Задача № 2: найти все пересечения прямолинейных отрезков;
Задача № 3: проверить, является ли многоугольник простым (многоугольник называется простым, если его контур не имеет самопересечений);
Задача № 4: проверить, пересекаются ли многоугольники.
Рассмотрим последовательность шагов построения математической модели при решении Задачи № 1.
Постановка задачи:
Дано: n прямолинейных отрезков на плоскости.
Требуется: определить факт пересечения хотя бы двух из них.
Ответ задачи – «да», если пересекаются, или «нет» в противном случае.
Разработка модели:
Установить факт пересечения пары отрезков можно в два этапа:
1. Определить факт пересечения ограничивающих прямоугольников каждого из отрезков (грубый тест).
Уточнение № 1: ограничивающий прямоугольник отрезка является наименьшим из прямоугольников, содержащих отрезок и имеющих стороны, параллельные осям координат.
Уточнение № 2: если ограничивающие прямоугольники не пересекаются, то и отрезки не пересекаются, если же установлен факт пересечения ограничивающих прямоугольников, то следует перейти ко второму этапу и проверить собственно пересечение отрезков (точный тест).
2. Если на первом этапе отсутствие пересечения двух отрезков не установлено тестом на пересечение ограничивающих прямоугольников, то необходимо применить точный тест.
В основе теста лежит следующее утверждение: два отрезка пересекаются тогда и только тогда, когда каждый из отрезков пересекается с прямой, содержащей другой отрезок.
Уточнение № 3: отрезок пересекается с прямой, если концы отрезка лежат по разные стороны относительно прямой или на прямой (хотя бы один конец).
Уточнение № 4: определить, лежит ли точка q=(xq,yq) по левую или по правую сторону относительно прямой или на прямой, содержащей ориентированный отрезок [p1,p2], можно, анализируя знак ориентированной площади S(p1,p2,p3)=½(x1-x2)(yq-y1)-(y2-y1)(xq-x1) треугольника p1p2q (или, что тоже, векторного произведения p1p2 x p1q).
Уточнение № 5: граничные случаи, когда хотя бы один из концов одного отрезка лежит на прямой, содержащей другой отрезок, и, следовательно, хотя бы одна из ориентированных площадей равна нулю, требуют дополнительного анализа.
Уточнение № 6: в тех случаях, когда кроме факта пересечения пары отрезков требуется определить точку их пересечения, данную модель следует дополнить, используя параметрические уравнения отрезков.
Модель нахождения пересечения отрезков была реализована в среде Microsoft Visual Studio на языке программирования С#. При реализации данной математической модели был разработан вспомогательный класс – segment, в котором были выполнены следующие вспомогательные структуры:
1) нахождение ограничивающего прямоугольника (НОП) для заданного отрезка;
2) проверка пересечения прямоугольников (ППП);

3) вычисление ориентированной площади (ВОП);
4) классификации точки относительно отрезка (Необходима при рассмотрении граничных случаев);
5) нахождение точки пересечения отрезков (НТПО).
Уточнение № 7: в случаях, когда хотя бы один из исходных отрезков вертикален или горизонтален, алгоритмы НОП и ППП дают правильный результат.
Уточнение № 8: в случаях, когда факт пересечения отрезков установлен, а отрезки «накладываются друг на друга» – имеют некоторую одинаковую часть, то алгоритм нахождения точки пересечения отрезков работает некорректно.
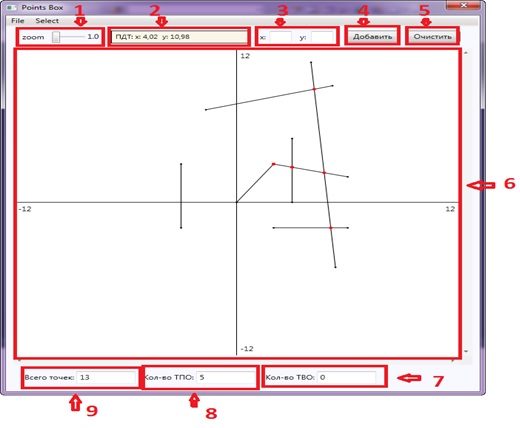
Интерфейс финальной версии проекта получил следующий вид (см. Рис.1):
Рис. 1. Интерфейс проекта
(1–масштабирование поля; 2–координаты последней добавленной точки; 3–пользовательские координаты точки; 4–кнопка добавления точки на поле; 5–кнопка очистки поля; 6–рабочее поле; 7–количество точек выпуклой оболочки (другая задача); 8–количество точек пересечений отрезков; 9–общее количество точек).
Задачи, выделенные в предметной области «Вычислительная геометрия “Пересечение отрезков”» являются хорошим фундаментом для формирования и совершенствования профессиональных навыков будущих математиков-программистов, так как требуют не только знаний в области языков программирования, но и математических знаний, в данном случае из области геометрии. Описанная модель нахождения пересечения пары отрезков является базовой в алгоритмах нахождении всех пересечений отрезков. Изучение данной модели может служить основой для построения более сложных алгоритмов вычислительной геометрии, например таких, как метод заметания плоскости прямой линией.
Библиографический список
- Мартынюк Ю.М., Использование математического моделирования при обучении программированию/Мартынюк Ю.М., Ванькова В.С., Ваньков Б.П. // Современная педагогика. 2014. № 11 (24). С. 41-44.
- Мартынюк, Ю.М. Обучение школьников программированию через систему творческих задач|/Мартынюк Ю.М., Ванькова В.С., Даниленко С.В.// Современные научные исследования и инновации. 2015. № 7-4 (51). С. 76-80.