Начертательная геометрия служит теоретической основой для создания чертежа – гениального изобретения человечества. Традиционно изучение этой дисциплины направлено на формирование навыков восприятия и создания конструкторского документа – чертежа как одного из  видов инженерно-графической информации [2].

Решение  многих инженерных задач  можно  производить  графически и аналитически, при  этом  всегда нужно предпочитать наиболее  целесообразный  и рациональный метод. Многие задания выполняются графически проще и быстрее, чем аналитически. Метод начертательной геометрии – это графический метод. Знание основных теорем и правил позволяет решать сложные ненормализованные задачи путем разделения процесса их выполнения на однотипные элементарные операции. Эта дисциплина лучше всего развивает у студента логическое мышление, пространственное воображение, пространственного воображения, без которых невозможно вообразить любое инженерное творчество.

Для  успешного  изучения и освоения  данной дисциплины студенты  должны  иметь приличные знания  в  области геометрии. Ещё  в школе они должны были усвоить основные положения, относящиеся  к  взаимному  положению  прямых в  пространстве, относительному расположению плоскости и прямой, двух плоскостей общего и частного положения, определению натуральной величины углов между плоскостью и прямой и двумя плоскостями. Начертательная  геометрия  является  для  студентов  абсолютно новой  дисциплиной, особенно трудно дающейся тем,  у кого не было в школе черчения. Здесь вводится большое  количество  новых терминов, обозначений, условностей.

Для будущего инженера необходимо хорошее пространственное мышление, пространственное воображение. Благодаря начертательной геометрии все это развивается.

Требования, предъявляемые к качеству графической подготовки выпускников, вызывают необходимость поиска путей совершенствования  методов обучения.

Предлагается разрабатывать задания на стыке геометрии и начертательной геометрии.

Например, определение натуральной величины треугольника двумя способами. Графическим способом – с помощью геометрических построений и аналитическим – с использованием формул и вычислений.

Определим натуральную величину треугольника графическим методом.

Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, один катет которого равен одной из проекций отрезка, а другой – разности расстояний концов второй проекции от плоскости проекций.

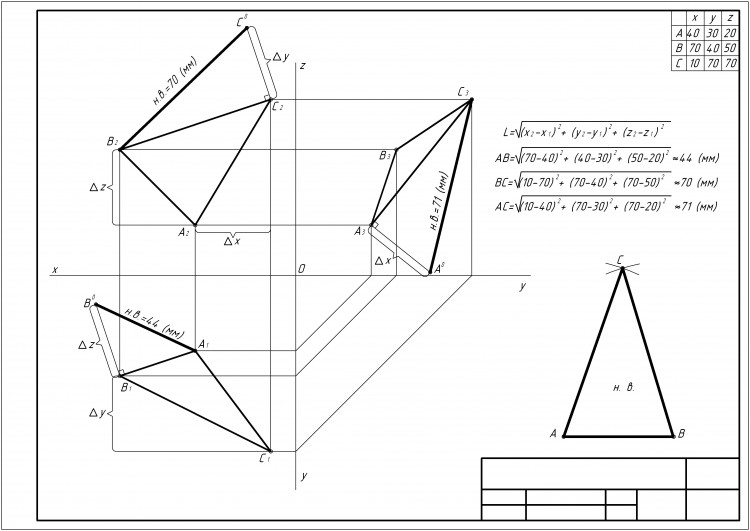
Для того, чтобы найти натуральную величину стороны AB треугольника (рис. 1) строим прямоугольный треугольник A₁B₁B⁰. Его первый катет A₁B₁ – это горизонтальная проекция стороны AB. Второй катет B₁B⁰ равен разности Δz (z_B – z_A), т. е. разности удаления точек A и B от горизонтальной плоскости π₁. Гипотенуза A₁B⁰ – натуральная величина стороны AB данного треугольника.

Рис. 1

Для наглядности натуральную величину стороны BC определим на фронтальной плоскости проекций, а стороны AC – на профильной (см. рис. 1).

С помощью циркуля построим натуральную величину треугольника ABC, зная длины трех его сторон (см. рис. 1).

Определим длины сторон треугольника аналитически по формуле (см. рис. 1).

где x₁, y₁, z₁, x₂, y₂, z₂ – координаты первого и второго конца отрезка соответственно.

Сравним полученные результаты.

Таким образом мы определили стороны треугольника, используя знания геометрии и начертательной геометрии. Это позволяет студенту вспомнить школьный курс геометрии и быть уверенным в правильности выполнения задания методом прямоугольного треугольника.

1. Вольхин К.А., Лейбов А.М. Проблемы формирования  графической компетентности в системе высшего профессионального образования // Философия образования. 2012. № 4. С. 16–22.

Все статьи автора «Иванов Алексей Юрьевич»