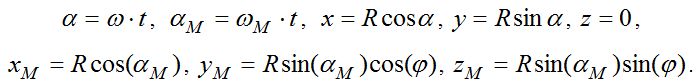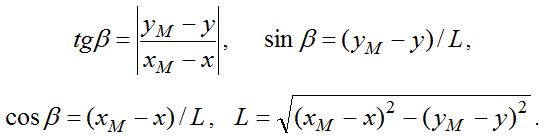Развитие цифровой педагогики предполагает разработку простых компьютерных моделей различных явлений природы, которые были бы понятны студентам и школьникам. Это относится и к физическим, и к астрономическим явлениям. Понятно, что метод компьютерного моделирования [4] целесообразно применять тогда, когда другой способ не позволяет решить поставленную задачу и изучить поведение рассматриваемой системы. Примером проблемы, требующей использования компьютерных моделей, является задача о расчете траектории движения планет по небесной сфере.
С древних времен известно, что планеты в течение года перемещаются относительно других звезд и выписывают на небесной сфере петли или зигзагообразные линии. Это явление объясняется вращением Земли (а значит и наблюдателя) и планет вокруг Солнца с различными скоростями. Земля движется быстрее верхних планет (Марса, Юпитера, Сатурна и т.д.), но медленнее нижних планет (Меркурия и Венеры) [2, 3]. Когда Земля и планета оказываются по одну сторону от Солнца, планета останавливается на небесной сфере и начинает совершать попятное движение, перемещаясь с востока на запад. Через некоторое время планета изменяет свое движение на прямое. Средние угловые размеры дуг попятного движения имеют значения [3, с. 57]: для верхних планет: Марс – 15, Юпитер – 10, Сатурн – 7, Уран – 4 Нептун – 3 Плутон – 2; для нижних планет: Меркурий – 12, Венера –16.
Понятно, что перемещение планеты по небесной сфере зависит от: 1) размеров ее орбиты и орбиты Земли; 2) скоростей движения планеты и Земли; 3) угла между плоскостью орбиты планеты и плоскостью эклиптики; 4) удаленности Земли и планеты от линии узлов. Расчет движения планеты –– безусловно интересная задача, которая полезна для студентов, изучающих астрономию. В настоящее время существуют различные компьютерные модели Солнечной системы [6, 7], позволяющие изучить целую совокупность астрономических явлений, начиная от Солнечных и Лунных затмений и заканчивая прохождением той или иной кометы мимо Юпитера. Они созданы профессиональными программистами и имеют несомненные преимущества. В то же время большой интерес представляет компьютерное моделирование движения планеты, расчет ее перемещений по небесной сфере с помощью простых программ, созданных студентами или преподавателями в рамках учебно–исследовательской работы по астрономии.
2. Движение Марса по небесной сфере
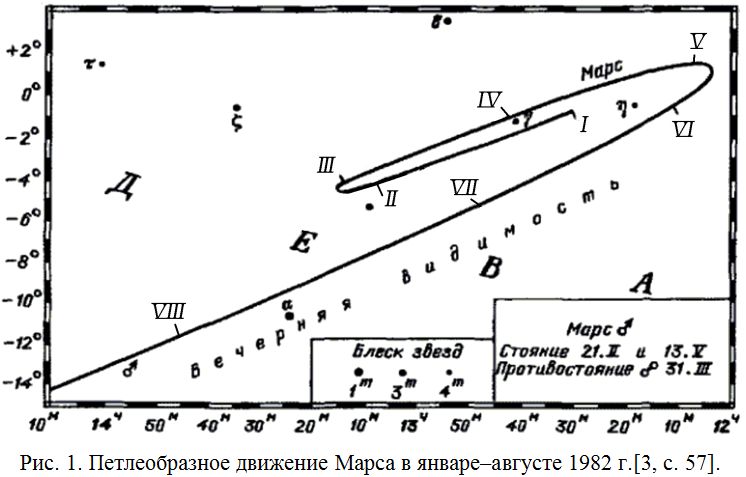
Вот как описывается перемещение верхней планеты в учебнике Кононовича Э.В. и Мороза В.И. [3]. “Когда верхняя планета видна после захода Солнца на западном небосклоне, она перемещается среди звезд прямым движением, то есть запада на восток, как и Солнце. Но скорость ее движения меньше чем у Солнца, которое постепенно нагоняет планету, и она на некоторое время перестает быть видимой, так как восходит и заходит почти одновременно с Солнцем. Затем, когда Солнце обгонит планету, она становится видимой на востоке перед восходом Солнца. Скорость ее прямого движения постепенно уменьшается, планета останавливается и затем начинает перемещаться среди звезд попятным движением, с востока на запад (рис. 1). Через некоторое время планета снова останавливается, меняет направление своего движения на прямое, снова ее с запада нагоняет Солнце, и она опять перестает быть видимой – и все явления повторяются в том же порядке” [3, с. 56–57].
Рассмотрим перемещения верхней планеты на примере Марса. На рис. 1 и 2 представлены петлеобразная и зигзагообразная траектории Марса на небесной сфере. Попятное движение длится около двух месяцев. Середина дуги попятного движения внешней планеты соответствует ее противостоянию с Солнцем, то есть такому положению, когда Земля находится точно между Солнцем и планетой. Например, в 2014 году Марс совершал попятное движение с 1 марта по 20 мая (даты стояния планеты), причем 9 апреля наступило противостояние. Середина дуги прямого движения планеты, когда планета находится за Солнцем, отвечает конфигурации соединение.
Если бы Марс двигался точно в плоскости земной орбиты, то наклон его траектории на небесной сфере объяснялся бы исключительно наклоном земной оси к плоскости эклиптики. При этом он перемещался бы по прямой линии без зигзагов или петель, также дважды останавливаясь и совершая попятное движение во время противостояния. На самом деле плоскость орбиты Марса составляет небольшой угол с плоскостью эклиптики (рис. 3.1). Поэтому, когда Земля и Марс находятся в противостоянии вблизи линии узлов NN’ (точки З0 и M0), получается зигзагообразная траектория, так как геоцентрическая широта Марса (угол между направлением Земля–Марс и плоскостью эклиптики), монотонно увеличивается или уменьшается. Если Земля и Марс находятся в противостоянии далеко от линии узлов NN’ (точки A1 и B1), то Марс по небесной сфере перемещается по петлеобразной кривой потому, что его геоцентрическая широта сначала растет, а затем уменьшается (или наоборот).
3. Расчет движения Марса
Зная законы движения Земли и Марса, рассчитаем движение Марса относительно системы отсчета, связанной с Землей. Для решения этой кинематической задачи и с целью упрощения рассуждений сделаем два предположения: 1) Земля и Марс движутся не по эллиптическим, а по круговым орбитам; 2) ось вращения Земли перпендикулярна плоскости ее орбиты (плоскости эклиптики), которая в этом случае совпадает с плоскостью небесного экватора. Тогда геоцентрическая широта Марса будет равна его склонению, а геоцентрическая долгота – прямому восхождению (или отличаться на константу). Следует учесть, что звездный период обращения Марса 1,88 года, радиус орбиты 1,52 а.е., наклонение орбиты к плоскости эклиптики 1,85. Угловая скорость орбитального движения Земли 6,28 рад/год, а Марса – в 1,88 раз меньше.
Удобно использовать систему координат OXYZ (рис. 3.1), оси OX и OY которой лежат в плоскости эклиптики (земной орбиты). Марс обращается по окружности радиусом 1,52 а.е., лежащей в плоскости OXY’, которая составляет угол YOY’=1,85 градусов с плоскостью эклиптики OXY. Ось OX совпадает с линией узлов NN’. В нашем случае с целью упрощения рассуждений гелиоцентрическую долготу a_m и геоцентрическую долготу beta Марса будем отсчитывать от оси OX (то есть линии узлов). Обычно эти углы отсчитываются от направления на точку весеннего равноденствия.
Земля и Марс движутся практически равномерно, их гелиоцентрические долготы, равные углам NOЗ и NOM (рис. 3.1 и 3.2), увеличиваются прямо пропорционально времени. Координаты Земли и Марса изменяются в соответствии с уравнениями:
Расстояние L между проекциями планет на плоскость эклиптики XOY и геоцентрическая долгота могут быть найдены из уравнений:
В рамках используемой модели плоскость эклиптики совпадает с небесным экватором и геоцентрическая широта Марса (угол между направлением Земля–Марс и плоскостью земной орбиты) равна его склонению. Так как для Земли всегда z=0, то геоцентрическая широта Марса может быть вычислена по формуле: gamma=arctg(z_m/L).
4. Компьютерная программа и результаты моделирования
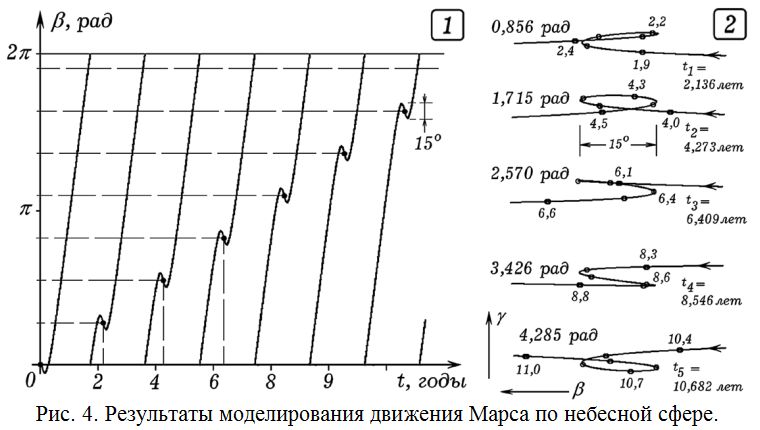
Для расчета траектории движения Марса по небесной сфере используется программа ПР–1, написанная в среде Free Pascal [5]. Она вычисляет геоцентрическую долготу и широту Марса через заданное время от начала отсчета, когда планеты находились на линии узлов (точки З0 и М0). Получающийся график зависимости геоцентрической долготы Марса от времени представлен на рис. 4.1. Из него следует, что большую часть времени Марс движется в прямом направлении, геоцентрическая долгота возрастает. Зигзаги соответствуют движению Марса в обратном направлении, а жирные точки – положениям Марса в моменты противостояния. Видно, что Земля и Марс оказываются в противостоянии через 2,136 лет; эта величина называется синодическим периодом. Каждое новое противостояние повернуто относительно предыдущего на 0,856 рад или 49 градусов. Чтобы получить эти значения, необходимо отключить графический режим и вывести на экран значения a, a_m и t в те моменты, когда гелиоцентрические долготы планет примерно одинаковы (a=a_m). Для этого в программе ПР–1 достаточно раскомментировать условный оператор, содержащий writeln(…).
Чтобы получить траекторию Марса на небесной сфере строят последовательность его положений в системе координат “геоцентрическая долгота– геоцентрическая широта” (рис. 4.2). Так как в эти моменты времени положение Марса по отношению к плоскости эклиптики, а значит и геоцентрическая широта различны (из-за наклона плоскости его орбиты), то выписываемые им траектории на небесной сфере также отличаются своей формой. Для их получения следует задавать различные смещения по геоцентрической долготе (переменная Sm). Программа определяет положение Марса в заданные моменты времени (например, при t = 1,9; 2,0; 2,1; 2,2; 2,3; 2,4 года) и строит его траекторию в соответствующем временном интервале.
Из получающихся результатов видно, что Марс выписывает петлю во втором и пятом случаях (рис. 4.2). Им соответствуют противостояния Земли и Марса в моменты t_2 = 4,273 года и t_5 = 10,628 лет при гелиоцентрических долготах 1,715 рад (98 градусов) и 4,285 рад (246 градусов). При этом Марс и Земля повернуты относительно линии узлов на 98 и 66 градусов соответственно. Зигзагообразные траектории получаются, когда Земля и Марс находятся достаточно близко к линии узлов. Если на экране построить деления через 5 градусов, то можно установить, что длина дуги, соответствующей обратному ходу Марса, составляет примерно 15 градусов.
Получающиеся траектории Марса очень похожи на наблюдаемые (рис. 1 и 2), но не имеют такого наклона к небесному экватору. Это объясняется тем, что небесный экватор образует угол 23 градуса с плоскостью эклиптики. При решении задачи предполагалось, что земная ось перпендикулярна плоскости эклиптики, а небесный экватор совпадает с ней.
5. Заключение
В настоящей статье рассмотрен метод расчета траектории движения Марса по небесной сфере и предложена несложная компьютерная программа на языке Pascal, которая позволяет решить следующие задачи: 1) промоделировать вращение Земли и Марса вокруг Солнца и установить синодический период Марса; 2) задав гелиоцентрические долготы Земли и Марса в начальный момент определить гелиоцентрические долготы этих планет, а также геоцентрические долготу и широту Марса в заданный момент времени (например, когда наступает противостояние); 3) рассчитать траекторию движения Марса по небесной сфере в заданный промежуток времени; 4) определить длительность и угловой размер дуги попятного движения Марса. Решение перечисленных задач на занятиях по астрономии позволяет объяснить студентам сложный характер движения планет по небесной сфере, а также познакомить их с методами компьютерного моделирования. Рассмотренная компьютерная модель может быть также использована при выполнении студентами или школьниками учебного исследования.
Библиографический список
- Астрономический календарь. Ежегодник. 1984. – Москва: Наука, 1983. – 319 с.
- Воронцов–Вельяминов Б.А., Страут Е.К. Астрономия. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2004. – 224 с.
- Кононович Э.В., Мороз В.И. Общий курс астрономии: Учебное пособие. – М.: Едиториал УРСС, 2004. – 544 с.
- Майер Р.В. Компьютерное моделирование физических явлений. – Глазов: ГГПИ, 2009. – 112 с.
- Попов В.Б. Turbo Pascal для школьников: Учеб. пособие. – М.: “Финансы и статистика”, 2001. – 528 с.
- http://www.solarsystemscope.com/ru – Модель Солнечной системы
- http://v-kosmose.com/interaktivnaya-2d-i-3d-model-solnechnoy-sistemyi/ – Интерактивная модель Солнечной системы