При подготовке бакалавров одним из актуальных вопросов является определение методических подходов к подбору задач с прикладным содержанием. Ниже предлагаемый подход иллюстрируется на примере фундаментальной подготовки в рамках бакалавриата по ФГОС 3+ по направлению 08.03.01 – Строительство.
1. Чтобы выпилить из цилиндрического бревна наименее прогибающуюся прямоугольную балку, на торце бревна проводят диаметр АВ, делят его на три равные части и из точек деления С и D проводят перпендикуляры к диаметру. Прямоугольник AEBF (почему это прямоугольник?) принимают за основание искомой балки. Докажите правомерность такого способа, приняв к сведению, что сопротивление изгибу прямо пропорционально произведению ширины на квадрат высоты сечения балки.
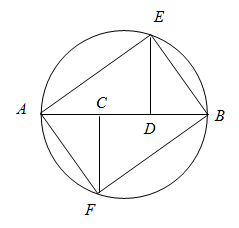
Пусть d – диаметр бревна; х – ширина, а h – высота выпиленной из бревна прямоугольной балки. При любых х и h справедливо:
Тогда сопротивление изгибу равно:
Функция F принимает наибольшее значение на [0,d] при ![]() , т.е. при
, т.е. при ![]() .
.
Так что балка должна иметь ширину ![]() и высоту
и высоту ![]() (
(![]() ). Именно к такому отношению размеров и приводит описанный выше практический способ. Действительно, воспользовавшись тем, что катет есть среднее пропорциональное между гипотенузой и своей проекцией на гипотенузу, получим:
). Именно к такому отношению размеров и приводит описанный выше практический способ. Действительно, воспользовавшись тем, что катет есть среднее пропорциональное между гипотенузой и своей проекцией на гипотенузу, получим:
откуда следует, что ![]()
2. По двум улицам движутся к перекрестку две автомашины с постоянными скоростями и1 и и2. Считая, что улицы пересекаются под прямым углом, и зная, что в некоторый момент времени автомашины находятся от перекрестка на расстояниях а1 и а2 определить, через какое время расстояние между ними станет наименьшим.
Первая машина за время t будет находиться от перекрестка на расстоянии ![]() , вторая – на расстоянии
, вторая – на расстоянии ![]() . Так что, расстояние l между машинами определится в виде
. Так что, расстояние l между машинами определится в виде
Имеем
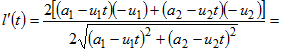
.gif)
При ![]() имеем
имеем ![]() .
.
При переходе через t1 ![]() меняет знак с минуса на плюс Следовательно, в момент t1 функция достигает минимума.
меняет знак с минуса на плюс Следовательно, в момент t1 функция достигает минимума.
Отметим, что знаменатель ![]() может обратиться в нуль только при условии
может обратиться в нуль только при условии ![]() , что соответствует случаю, когда машины должны встертиться на перекрестке. Не рассматривая этот частный случай, можно утверждать, что
, что соответствует случаю, когда машины должны встертиться на перекрестке. Не рассматривая этот частный случай, можно утверждать, что ![]() в интервале (0;) имеет единственный эктремум (минимум). В силу предыдущего функция достигает своего наименьшего значения на указанном интервале в точке минимума.
в интервале (0;) имеет единственный эктремум (минимум). В силу предыдущего функция достигает своего наименьшего значения на указанном интервале в точке минимума.
3. Требуется огородить забором прямоугольный участок площадью S=1,5 га и затем разделить его таким же забором на две равные части. Определить размеры участка, при которых расход материалов на ограждение будет наименьшим.
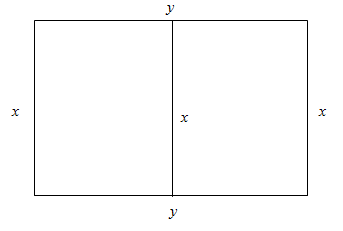
1-й способ решения.
Примем за критерий эффективности общую длину забора
По условию xy=15000 м2, следовательно, ![]() , тогда
, тогда
Для определения lmin найдем ![]() :
:
Нетрудно проверить, что при x=100 м будет lmin.
Действительно, ![]()
2-й способ решения.
Составим функцию Лагранжа
.gif)
.gif)
.gif)
4. Указать размеры прямоугольного параллелепипеда наибольшего возможного объема, вписанного в прямой круговой конус с радиусом основания R и высотой Н.
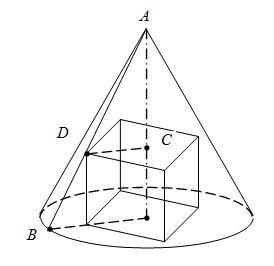
Обозначим размеры основания параллелепипеда через х и у и высоту через z. Тогда объем V=xyz. Используя то, что параллелепипед вписан в данный конус, можно найти соотношение между x, y, z, H и R. Действительно, из подобия треугольников ОАВ и CAD находим:
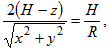
откуда ![]() . Подставляя выражение для z в формулу объема, получим объем параллелепипеда как функцию двух переменных х и y:
. Подставляя выражение для z в формулу объема, получим объем параллелепипеда как функцию двух переменных х и y:
Из рисунка видно, что х и у должны удовлетворять неравентсву
Таким образом, надо найти наибольшее значение ![]() в замкнутой области (круг радиуса 2R).
в замкнутой области (круг радиуса 2R).
Найдем стационарные точки внутри области:
.gif)
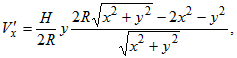
откуда ![]() и
и ![]()
![]() . (Значения х=0 и у=0 не рассматриваем, так как в этом случае V=0.) Тогда
. (Значения х=0 и у=0 не рассматриваем, так как в этом случае V=0.) Тогда ![]() Объем при таких размерах равен:
Объем при таких размерах равен: ![]() . Исследуем функцию
. Исследуем функцию ![]() на границе области. Если
на границе области. Если ![]() , то V=0. Следовательно, полученные выше размеры
, то V=0. Следовательно, полученные выше размеры ![]() и
и ![]() дают действительно наибольший искомый объем.
дают действительно наибольший искомый объем.
Направленность всех приведенных примеров на формирование общепрофессиональных компетенций очевидна. С учетом междисциплинарных связей фундаментальная подготовка бакалавров, исходя из непрерывности образования, может осуществляться и при изучении дисциплин как общепрофессионального, так и профессионального модуля, а также дисциплин по выбору.
Библиографический список
- Гарькина И.А., Данилов А.М. Системный подход к повышению качества образования / Вестник КГУ им. Н.А. Некрасова. – 2013. – №4. – Т. 19. – С. 4-7
- Данилов А.М., Гарькина И.А., Маркелова И.В. Междисциплинарные связи при компетентностном подходе к подготовке бакалавров // Современные проблемы науки и образования. – 2014. – № 3;URL: http://www.science-education.ru/117-13065
- Данилов А.М., Гарькина И.А., Маркелова И.В. Методологические принципы оценки качества образовательной системы / Современные проблемы науки и образования. – 2014. – № 2. URL: http://www.science-education.ru/116-12335
- Данилов А.М., Гарькина И.А. Образовательная система с позиций идентификации и управления / Региональная архитектура и строительство. – 2013. – № 2. – С. 143-146.
