Введение
Важным источником учебного материала для ученика является учебник, его содержание и структура фактически определяют последовательность изучения различных вопросов соответствующей дисциплины. Информация, изложенная в учебниках, ее сложность и уровень абстрактности должна соответствовать современному содержанию науки и психологическим особенностям развития учащихся, их способностям усваивать и осмысливать получаемые знания. Решение этой проблемы требует совершенствования объективных методов измерения количества различных видов информации в учебных текстах, оценки сложности и уровня абстрактности изложения материала [1 – 6]. Для определения количества информации мы будем применять объемный подход, состоящий в подсчете числа использований научных терминов (названий объектов, явлений, физических величин и т.д.), и математических символов.
1. Эмпирические, теоретические и математические знания
Как известно, метод контент–анализа состоит в “переводе в количественные показатели массовой текстовой информации” и их последующей статистической обработке [1]. Основой для проведения контент–анализа учебного физического текста является классификация знаний на эмпирические, теоретические и математические. Эмпирическими называются знания об объектах и происходящих с ними явлениях, полученные как результат чувственных ощущений в процессе выполнения наблюдения или эксперимента. Теоретические знания –– это знания сущности объектов и явлений, получающиеся в результате обобщения опытных данных или конкретизации общих положений науки. Математические знания включают в себя математические термины, формулы, а также изображения математических объектов на рисунках.
Понятно, что перечисленные виды знаний в некоторых случаях не поддаются четкому и однозначному разделению в силу объективных причин. Качественные объяснения наблюдаемых явлений (элементы теоретических знаний) могут содержать большое количество “эмпирических” терминов, обозначающих объекты и явления, приборы и устройства. Обычно это относится к простым вопросам, изучаемым в 7 – 8 классах. В этой ситуации наличие “эмпирических” терминов показывает невысокий уровень абстракции (сложности) учебного материала.
Следуя принципу “измерять то, что можно измерить” [1], при анализе текста будем подсчитывать число использований “эмпирических” терминов (обозначающих объекты и явления, приборы и устройства), “теоретических” терминов (названия физических величин), математических терминов (математические величины, операции, символы в формулах) и общенаучных терминов (“докажем”, “измерения”, “проанализируем” и т.д.). Получающиеся частоты употребления соответствующих терминов характеризуют объем Э–знаний, Т– М– и Н–знаний в тексте.
Рассматриваемый подход достаточно формален и не позволяет оценить содержательную сторону учебной информации, правильность логических выводов, методическую обоснованность рассуждений и т.д. Однако эта задача и не ставится. Предполагается, что анализируемый учебник соответствует всем предъявляемым требованиям [2, 6], и проблема состоит в определении сложности и количества различных видов информации в том или ином параграфе.
2. Абстрактность изложения и сложность текста
Хорошо известно, что изучение школьных дисциплин естественно–научного цикла, и в первую очередь физики, требует от школьников развитого абстрактного мышления. Даже рассмотрение механических и тепловых явлений предполагает использование идеализированных моделей (материальная точка, идеальный газ) и разнообразных математических абстракций (система отсчета, вектора и их проекции, графики и т.д.). При изучении основ электродинамики, оптики, атомной и ядерной физики школьники вынуждены представлять в своем воображении различные объекты (электромагнитные волны, атомы, элементарные частицы) и явления (фотоэффект, ядерная реакция), которые не воспринимаются органами чувств и невозможно пронаблюдать в повседневной жизни.
Степень отвлеченности используемых понятий и проводимых рассуждений характеризуется уровнем абстракции. В зависимости от конкретной задачи можно изучать один и тот же объект на различных уровнях абстракции. В теории познания абстрактное противопоставляется конкретному. К самому низкому уровню абстракции относится конкретная вещь, воспринимаемая органами чувств (данная пружина, именно этот динамометр, конкретный вольтметр). Более высоким уровнем абстракции является понятие родовой сущности вещи (“амперметр вообще”). Следующий уровень соответствует использованию в своих рассуждениях идеализированных моделей (капельная модель ядра) или объектов (фотон, атомное ядро), которые нельзя пронаблюдать в повседневной жизни или в физической лаборатории. Высокую степень абстрактности имеют математические модели (число 7, плоскость, график колебаний). Восхождение от конкретного к абстрактному приводит к созданию качественной, а затем и количественной теории. Для школьного курса физики наивысшую степень абстрактности имеет математическая теория, включающая в себя сложные формулы с интегралами и производными.
Некоторые методы оценки абстрактности изложения в учебных текстах проанализированы в [6, c. 43 – 46]. Понятно, что чем больше в тексте встречается абстрактных понятий, тем выше его объективная сложность. Поэтому для оценки сложности эмпирической или теоретической информации необходимо оценить степень абстрактности всех встречающихся в тексте терминов, и частоту их использования.
3. Оценка сложности различных элементов физического текста
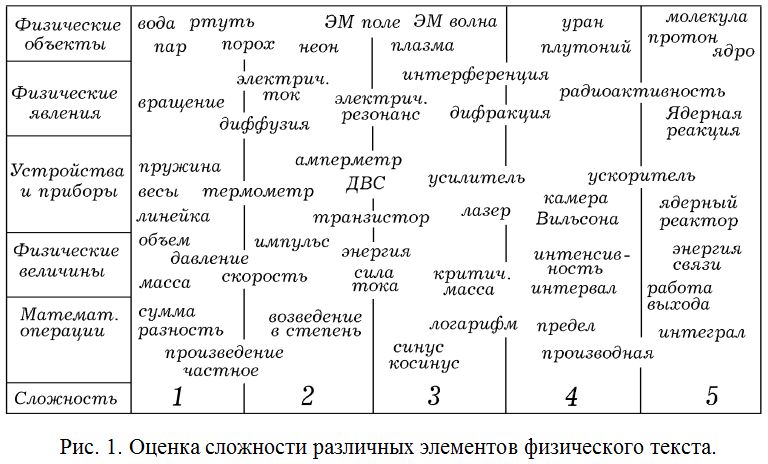
В учебных текстах используются научные термины, обозначающие физические объекты, явления, приборы, технические устройства и физические величины. С целью создания шкалы для оценки сложности физических величин автором был составлен список из 10 величин, взятых из различных разделов физики: масса, скорость, температура, внутренняя энергия, сила тока, индукция магнитного поля, длина волны, интенсивность, критическая масса, энергия связи. Использовался метод парных сравнений: величины сравнивались друг с другом, результаты записывались в таблицу 10 х 10. Если сложности сравниваемых величин примерно одинаковы, то в соответствующие клетки таблицы заносились нули, а если разные, –– то 1 и –1. Это позволило создать пятибалльную шкалу сложности физических понятий.
Методом парных сравнений, также была оценена сложность терминов, обозначающих физические объекты, явления, приборы, а также математических терминов и операций (рис. 1). При этом наименее сложными (S=1) считались термины, обозначающие явления, объекты или приборы, которые учащийся может пронаблюдать в повседневной жизни (вода), а наиболее сложными (S=5) –– термины, обозначающие объекты и явления, которые нельзя обнаружить с помощью органов чувств и для их изучения приходится напрягать воображение (ядро атома). Сложность объектов и явлений, которые можно пронаблюдать в физической лаборатории имеет промежуточное значение S=3. Для оценки сложности нового термина, не представленного на рис. 1, его необходимо сравнить с терминами, находящимися на рисунке, и отнести к одной из 5 категорий.
Приближенно, можно считать, что количество “формульной” информации пропорционально числу математических символов, встречающихся в тексте и в формулах. Каждый символ соответствует некоторой физической или математической величине. Поэтому для оценки количества М–знаний необходимо подсчитать число символов. При этом математические высказывания заменяются соответствующими предложениями минимальной длины, а затем подсчитывается число входящих в него ключевых слов. Например, для формулы s=vt (расстояние равно произведению скорости на время) I_m=5; формула Томсона для периода электромагнитных колебаний (период равен два пи корней из произведения индуктивности и емкости) I_m=8.
Важной характеристикой является сложность “формульной” информации, которая оценивалась по пятибальной шкале. При этом используются следующие критерии: 1. Сложность S=1: одиночные символы (не вектора) в тексте, равенство, сумма, разность, произведение и деление. 2. Сложность S=2: возведение в степень, извлечение корня, сложение и вычитание векторов. 3. Сложность S=3: тригонометрические функции, логарифмы, скалярное произведение векторов. 4. Сложность S=4: пределы, дифференциалы, производные, векторное произведение. 5. Сложность S=5: интегралы. Сложность формулы считается равной наибольшей сложности входящих в нее символов.
4. Результаты оценки сложности тем школьного курса физики.
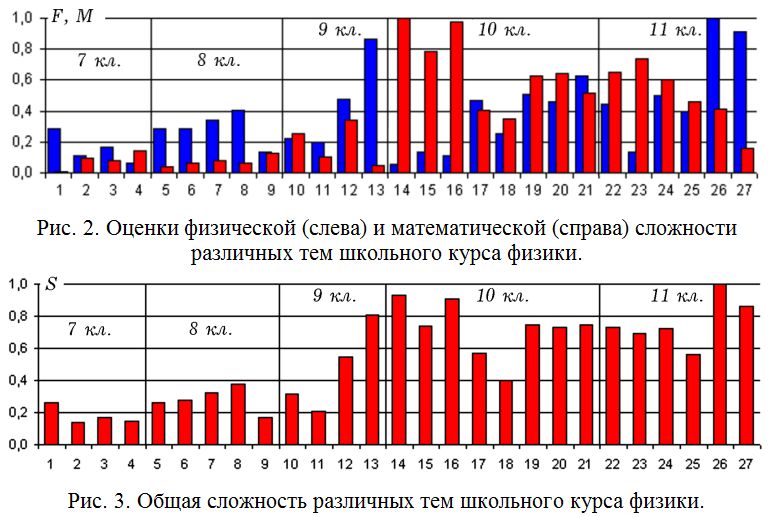
В результате анализа школьных учебников [7–11] за 7, 8, 9, 10, 11 классы были выделены 27 тем, которые включили в себя одну или несколько глав. В основе используемого метода лежат следующие предположения: 1) физическая сложность F достаточно большого учебного текста определяется сложностью физических объектов, явлений и экспериментов, изображенных на рисунках, а также сложностью используемых физических моделей; 2) математическая сложность M учебного текста достаточно большого объема зависит от количества рисунков, на которых изображены математические абстракции, числа и сложности формул. Поэтому нет необходимости детально анализировать текст, подсчитывать количество физических или математических терминов, учитывать их сложность и т.д., а достаточно проанализировать формулы и рисунки, оценить сложность рассматриваемых физических и математических моделей. По результатам оценки физической, математической и общей сложности тем школьного курса физики [7–11] построены гистограммы, изображенные на рис. 2 и 3 [4].
На рис. 4 изображено распределение тем школьного курса физики в пространстве, образованном осями F и M [4]. Числа, стоящие рядом с точками, совпадают с номерами учебников i в таблице 1. Темы, имеющие невысокую сложность, располагаются вблизи начала координат; наиболее сложным темам соответствуют точки, удаленные от начала координат. Видно, что в школьном курсе физики отсутствуют темы, для которых физическая и математическая сложности F_i и M_i одновременно больше 0,5. Это объясняется тем, что в школе при изучении сложных явлений квантовой физики (F велико), используются достаточно простые математические модели (M мало), а при изучении механики и молекулярной физики (F мало) –– наоборот сложные (M велико).
Все темы школьного курса физики можно разбить на четыре класса: 1) темы 1, 2, 3, 4 (7 класс), 5, 6, 7, 8, 9 (8 класс) и 11 с низкими F_i, M_i и S_i, образующие кластер вблизи начала координат; 2) темы 12, 19, 20, 21, 22, 24, 25 (электродинамика, оптика) и 17 (молекулярная физика) со средними F_i и M_i, образующие кластер в центральной части пространства; 3) темы 13, 26, 27 (теория относительности, физика микромира) с высокой физической сложностью F_i; 4) темы 14, 15, 16, 23 (механика) с высокой математической сложностью M_i.
5. Методика оценки количества различных видов информации
Для определения количества эмпирической, теоретической, математической и общенаучной информации в учебном тексте нами использовалась методика контент–анализа, изложенная в книге [1]. Были выбраны исчерпывающие и взаимоисключающие критерии, сформулировано правило для надежного фиксирования нужных характеристик текста так, чтобы получающиеся результаты не зависели от эксперта, имели высокую повторяемость и отражали объективные характеристики текста. Чтобы оценить количество информации в рисунках и формулах они заменялись максимально короткими предложениями, которые полно передают заключенную в них учебную информацию. Речь идет о полезной информации, необходимой для усвоения соответствующего параграфа учебника (ненужная информация, содержащаяся в рисунках не учитывается).
Нами в среде Free Pascal создана специальная программа Analyzer, которая, используя словарь–тезаурус, подсчитывает частоты упоминания различных физических и математических терминов в текстовом файле. Методика контент–анализа текста состоит из следующих этапов: 1. Определяют сложность и количество “формульной” информации путем подсчета числа математических символов в тексте и формулах. 2. Заменяют рисунки краткими описаниями, содержащими информацию об изображенных на рисунках физических и математических объектах. 3. Создают текстовый файл в формате data.txt, содержащий анализируемый текст с описаниями рисунков без формул. 4. Составляют список физических математических и общенаучных терминов, встречающихся в данном тексте. 5. Создают словарь–тезаурус текста, содержащий общие части однокоренных терминов (например, слова дифракция, дифрагировать, дифракционный –– общая часть “дифра”), который сохраняют в файле slovar.txt. 6. Каждый термин относят к одному из классов “эмпирический”, “теоретический”, “математический”, “общенаучный”, и оценивают его сложность S; результаты записывают в файл slovar.txt. 7. Запускают программу Analyzer, которая обращаясь к файлу slovar.txt, анализирует текст, хранящийся в файле text.txt, а результаты записывает в файл result.txt. Также создается профиль текста, состоящий из вектора наиболее часто встречающихся слов и вектора частот. 8. Интерпретируют результаты, создают таблицы, строят гистограммы и т.д.
В нашем случае единицей измерения объема информации является слово или одно упоминание термина. Так как в русском языке средняя длина слова 6,3 буквы (включая пробел), то для нахождения суммарного числа слов N (объема информации в тексте I) достаточно общее количество букв разделить на 6,3.
6. Примеры использования предлагаемой методики
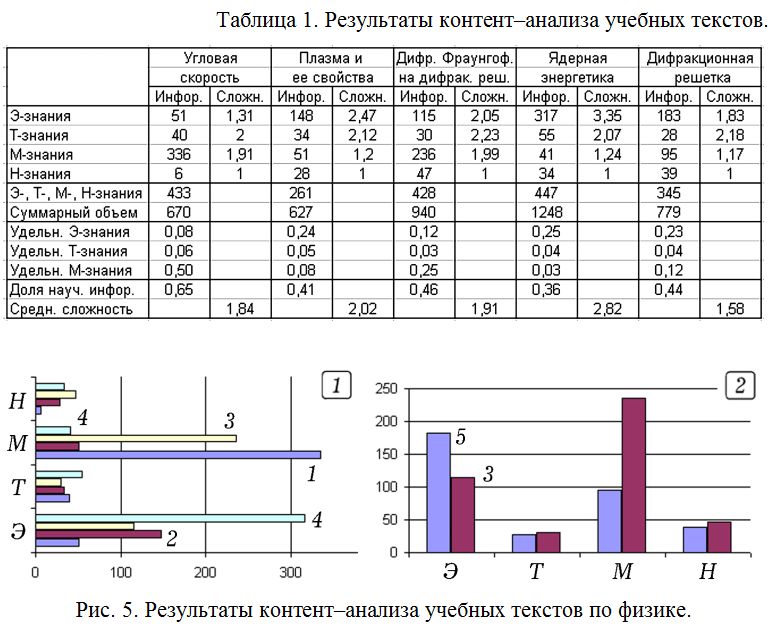
В качестве апробации были проанализированы четыре параграфа из вузовского учебника Трофимовой Т.И. [12] и одного параграфа из школьного учебника Мякишева Г.Я. [8]: 1) “Угловая скорость и угловое ускорение”; 2) “Плазма и ее свойства”; 3) “Ядерная энергетика”; 4) “Дифракция Фраунгофера на дифракционной решетке” [12]; 5) “Дифракционная решетка”[8]. При этом определялись сложность и объем эмпирической, теоретической, математической и общенаучной информации, объем научной информации, суммарный объем параграфа, доля научной информации, удельное количество Э–, Т–, М–знаний. Результаты представлены в таблице 1. Из нее, в частности, следует, что в параграфе “Угловая скорость и угловое ускорение” упоминаются: 1) “эмпирические” термины (объект–явление–прибор) –– 51 раза (средняя сложность –– 1,31); 2) “теоретические” термины (название физической величины) –– 40 раз (средняя сложность –– 2,0); 3) математические термины и символы 336 раз (средняя сложность –– 1,91); 4) общенаучные термины –– 6 раз (средняя сложность –– 1). Общий объем информации 670 слов, из них 433 упоминания научных терминов. Доля научной информации 0,65, средняя сложность –– 1,84.
Используемая компьютерная программа позволяет выявить наиболее часто встречающиеся термины (или их корни) и создать профиль анализируемого текста. На основе данных, представленных в таблице, может быть построена гистограмма (рис. 5), круговая или иная диаграмма, осуществлено сравнение проанализированных параграфов по сложности и количеству различных видов информации. Из рис. 5.1, соответствующего 4 параграфам учебника [12], видно, что наибольшее количество М–информации в параграфе ”Угловая скорость …”, а Э–информации –– в параграфе “Ядерная энергетика”. С помощью гистограммы на рис 5.2 можно сравнить параграфы “Дифракция Фраунгофера на дифракционной решетке” [12] и “Дифракционная решетка” [8]. Видно, что в школьном учебнике [8] больше эмпирической информации, а вузовском [12] –– математической. Количество Т– и Н–знаний в обоих случаях примерно одинаково.
Анализ представленных результатов (таблица 1, рис. 5) позволяет утверждать, что количества Э– и М–знаний являются важными характеристиками учебных текстов по физике, которые следует учитывать при классификации школьных параграфов и тем. Аналогичный вывод следует и из других исследований, выполненных автором [3–5].
Заключение
В настоящей работе рассмотрены: 1) методика оценки физической и математической сложности тем школьного курса физики; 2) методика оценки количества эмпирической теоретической математической и общенаучной информации в различных учебниках физики с помощью ПЭВМ. Кроме того, представлены получающиеся результаты, рассмотрено распределение тем школьного курса физики в пространстве признаков “физическая сложность F –– математическая сложность M”. Предложенная методика контент–анализа позволяет произвести сравнительный анализ учебников, тем, параграфов, установить закономерности распределения учебного материала.
Библиографический список
- Аверьянов Л.Я. Контент–анализ. –– Монография. –– М.: РГИУ, 2007. –– 286 с.
- Беспалько В.П. Теория учебника: Дидактический аспект. –– М.: Педагогика, 1988. –– 160 с.
- Майер Р.В. Автоматизированный метод оценки количества различных видов информации и ее сложности в физическом тексте с помощью ПЭВМ // Известия высших учебных заведений. N 3(31). –– 2014. –– C. 200–209.
- Майер Р.В. Классификация тем школьного курса физики на основе оценки их физической и математической сложности — Инновации в образовании. –– 2014. –– № 9. –– С. 29–38.
- Майер Р.В. Определение уровня абстрактности, сложности и информативности различных тем школьного учебника физики // Стандарты и мониторинг в образовании. –– 2013. –– Том 6, выпуск 1. –– С. 19–26.
- Микк Я.А. Оптимизация сложности учебного текста: В помощь авторам и редакторам. –– М.: Просвещение, 1981. –– 119 с.
- Мякишев Г.Я. Физика: Учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни / Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский. –– М.: Просвещение, 2004. – 336 с.
- Мякишев Г.Я., Буховцев Б.Б. Физика: Учеб. для 11 кл. общеобразоват. учреждений. –– М.: Просвещение, 2003. –– 336 с
- Перышкин А.В. Физика. 7 класс. Учебник для общеобразоват. учреждений. –– М.: Дрофа, 2003. –– 192 с.
- Перышкин А.В. Физика. 8 класс. Учебник для общеобразоват. учреждений. –– М: Дрофа, 2002. –– 192 с.
- Перышкин А.В., Гутник Е.М. Физика. 9 класс. Учебник для общеобразоват. учреждений. –– М.: Дрофа, 2005. –– 255 с.
- Трофимова Т. И. Курс физики: Учеб. пособие для вузов. — М.: Высш. шк., 2001. — 542 с.