Актуальность изучения возможностей применения Интернет-ресурсов в преподавании математических дисциплин связана: с увеличением объема Интернет-информации, нуждающейся в поиске, систематизации и использовании; с востребованностью специалистов владеющих математическими методами моделирования и умеющих проводить расчеты с использованием современного программного обеспечения; с необходимостью активного внедрения современных информационных технологий на занятиях по математике.
Особенности использования Интернет-ресурсов в преподавании математических дисциплин рассмотрены в работах Я. И. Мельниченко [1], В. С. Новиковой [2], Р. И. Остапенко [3], Е. В. Потехиной [4] и др. Авторами показано, что Интернет-технологии успешно используются в качестве символьного, наглядного, доступного средства обучения, а также обеспечивают многозадачность и дифференцированный подход в процессе обучения студентов.
В большинстве работ, под Интернет-ресурсом понимается какой-либо сайт (портал) имеющий электронные учебные пособия, журналы, энциклопедии, дающий возможность обработать данные в режиме онлайн, провести эксперимент или получить образование дистанционно. Под Интернет-ресурсом мы будем понимать сайт в сети Интернет, имеющий исходную информацию (данные) для решения математических задач.
Цель работы: рассмотреть методические аспекты использования Интернет-информации для решения практических задач в процессе преподавания математических дисциплин студентам вузов спортивной направленности.
Проблемы формирования математической и информационной компетентности студентов инженерно-технических, гуманитарных, естественнонаучных специальностей рассматриваются в целом [О.А.Велиханова [5], А.В.Кузьмина [6], Т.А.Лавина [7], так и в узкой специализации [Р.И.Баженов [8-14], Р.И.Остапенко [15-22], а в частности, студентов вузов спортивной направленности (Л. В. Архандеева [23]). Вопросы использования информационных технологий в обучении студентов вузов рассматриваются чаще всего без учета направления подготовки. Присутствует дефицит методических разработок по математической подготовке студентов вузов спортивной направленности.
Наблюдается терминологическая разобщенность в определении понятия «математическая компетентность» среди авторов. Это: и устойчивые математические знания, и умение применять их в новых ситуациях, и способность решать средствами математики профессиональных задач, и повышать свою квалификацию. Это и определенные ценностные ориентации специалиста, его мотивация, самооценка и т.д. Под математической компетентностью студента мы будем понимать сложное, системное свойство личности, опирающееся на наличие математических знаний, умений, навыков, способов деятельности и проявляющееся в готовности их использовать для эффективного решения различных профессиональных задач.
Нами были разработаны практические задачи для студентов различных специальностей вузов, проводимые при наличии компьютерных средств обучения и доступа к сети Интернет. В частности, разработаны методические указания для проведения аудиторных занятий и самостоятельных работ по курсам «Математика и информатика», «Математическая статистика» для студентов вузов спортивной направленности с использованием компьютеров и соответствующего программного обеспечения. Главные особенности методических разработок: преобладание активных методов и форм обучения, увеличение доли самостоятельной работы, включение студентов в исследовательскую деятельность и ориентация на их познавательную самостоятельность.
Процесс решения математических задач с использованием Интернет-ресурсов можно условно разбить на три этапа:
1. Поиск информации в Интернете ее и систематизация;
2. Обработка данных с помощью соответствующего программного обеспечения (MS Excel, SPSS, MathCAD и т.д.);
3. Интерпретация результатов, выводы.
Рассмотрим пример, где в качестве Интернет-ресурса (как источника для решения математических задач) выступает Официальный сайт Федерации лыжных гонок России [24], где, в частности, представлена база данных спортсменов, когда-либо принимавших участие во всероссийских соревнованиях, имеющих РУС и ФИС код (http://www.flgr.ru/rules/bd/). На 19 сентября 2013 года в базе состоит 9 358 человек. Файл базы данных представлен в формате Ms Excel.
Условие задачи. На основе заданной выборки спортсменов (для каждого студента индивидуально) средствами MS Excel:
1) вычислить средний возраст всей выборки;
2) подсчитать, сколько мужчин и женщин представлено в базе;
3) построить частотное распределение и график по спортивным разрядам;
4) установить зависимость между возрастом и спортивным разрядом выборки; составить регрессионную модель.
Описание решения. На начальном этапе данные скачиваются с сайта и подготавливаются для последующей обработки. В указанной выше базе для анализа данных используются шкалы «пол», «год рождения» и «разряд». Кратко опишем ход решения задачи на основе выборки из 1000 спортсменов.
1) Для нахождения среднего арифметического в MS Excel можно воспользоваться формулой: =2014-СРЗНАЧ(H2:H1001), моды: =2014-МОДА(H2:H1001), медианы: =2014-МЕДИАНА(H2:H1001). В указанной базе средние значения первой тысячи спортсменов равны: среднее арифметическое – 23,68 лет; мода – 18 лет, медиана – 22 лет.
2) Половой состав можно определить c помощью сортировки столбца с наименованиями пола «L» и «M» по возрастанию или убыванию и дальнейшим подсчетом числа мужчин и женщин с помощью функции =ЧСТРОК. В нашем примере, из 1000 спортсменов оказалось 377 женщин и 623 мужчины.
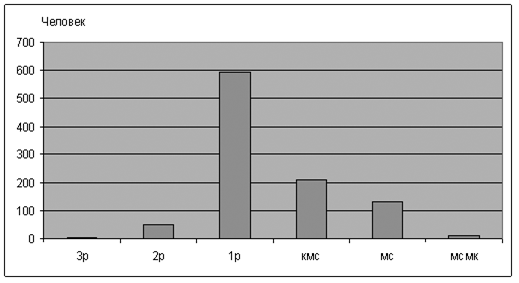
3) Построение частотного распределения и графика по спортивным разрядам состоит из двух этапов а) перекодировка текстовых ячеек «3р», «2р», «1р», «кмс», «мс», «мсмл» в ранговые с помощью вложенного условного оператора ЕСЛИ; б) построение гистограммы в помощью дополнительной надстройки Excel «Пакет анализа».
Перекодировка шести разрядов с помощью оператора ЕСЛИ имеет вид: =ЕСЛИ(I2=”3р”;1;ЕСЛИ(I2=”2р”;2;ЕСЛИ(I2=”1р”;3;ЕСЛИ(I2=”кмс”;4;ЕСЛИ(I2=”мс”;5;6))))). Частотное распределение и соответствующая гистограмма для нашего примера имеет вид:
Таблица 1. Частотное распределение спортсменов (1000 чел.) по спортивным разрядам
|
Карман |
Частота |
|
1 |
2 |
|
2 |
50 |
|
3 |
592 |
|
4 |
210 |
|
5 |
133 |
|
6 |
13 |
|
Сумма |
1000 |
Рис.1. Гистограмма частотного распределения выборки (1000 чел.) по разрядам
На графике частотного распределения видно, что большинство спортсменов имеют первый спортивный разряд (59,2%). Меньше всего лиц, имеющих третий спортивный разряд – 0,02% и мастеров спорта международного класса – 1,3%.
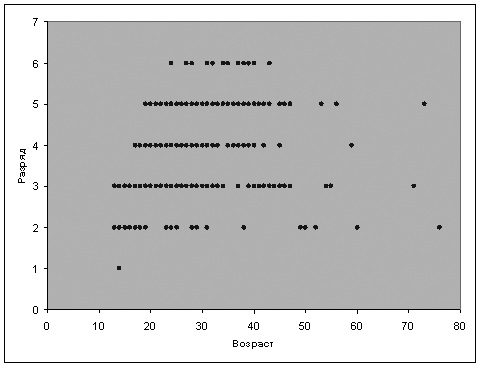
4) Установление зависимости между возрастом спортсменов и их спортивным разрядом проще всего начинать с построения простейшего двумерного точечного графика и нахождения коэффициента корреляции, а затем с помощью надстройки «Пакет анализа» проводить регрессионный анализ и составлять регрессионную модель. Обусловлено это тем, что, изначально, линейной связи может и не быть, поэтому корреляционно-регрессионный анализ будет излишним. Результат решения этой задачи студентами может быть оценен с использованием неформальных критериев, например, таких как: способность адекватно использовать математические методы, исследовательская интуиция и другие. В нашем примере коэффициент корреляции оказался равен + 0,44. Для выборки из тысячи человек он статистически значим, и получается, что чем старше спортсмен, тем выше его разряд. Однако, на двумерном графике (см. рис.2) связи возраста и разряда спортсменов видно, что в одном списке находятся спортсмены, возраст которых распределен от 15 до 75, т.е. выборка неоднородна и сопоставлять данные такого массива некорректно. Также, в одном списке, присутствуют мужчины и женщины, что влияет на объективность связи. В диапазоне данных можно внести ограничения, например, с помощью условия =ЕСЛИ(I2<30;I2;0) – в ячейке будет выводиться возраст до 30 лет, а в соответствующий столбец стажа ввести условие =ЕСЛИ(J2<>0;N2;0) для того, чтобы разряд выводился в столбце только для тех, кому меньше 30-ти. Результат этих ограничений показан на рисунке 3. Коэффициент корреляции для этой выборки равен + 0,51. По вопросу задачи необходимо составить регрессионную модель. Ее можно получить средствами MS Excel (см. табл.2)
Рис.2. Гистограмма связи возраста спортсменов (1000 чел.) с разрядом
Рис.3. Гистограмма связи возраста спортсменов (до 30 лет) с разрядом
Таблица 2. Показатели регрессии
| Y-пересечение |
1,938331652 |
| Переменная X 1 |
0,068735882 |
Теперь можно составить регрессионную модель вида Y = kX + b:
Разряд = Возраст * 0,07 + 1,94.
Коэффициент детерминации (R-квадрат) приблизительно составил 0,29 или 29%. Это означает, что модель плохо объясняет изменчивость уровня разряда от возраста, так как 71% – доля изменчивости уровня разряда, объясняемая другими факторами, а не возрастными.
Таким образом, методическая система преподавания математических дисциплин студентам вузов помимо информационных ресурсов, автоматизированных обучающих и компьютерных математических систем и сред должна включать Интернет-ресурсы как источник возникновения интерактивных задач. Одной из приоритетных задач в данной области выступает изучение особенностей организации работы студентов по решению задач при изучении математических дисциплин, разработка основных этапов реализации методической системы.
Библиографический список
- Мельниченко Я.И. Личностно-ориентированный подход к организации самостоятельной работы студентов с использованием интернет-ресурсов: дис. … канд. пед. наук: 13.00.01. – Орел, 2008. – 249 с.
- Новиков В.С. Использование компьютерных сетевых технологий для организации самостоятельной работы студентов при обучении математике: дис. … канд. пед. наук: 13.00.02. – Орел, 2006. – 209 с.
- Остапенко Р.И. Использование Интернет-ресурсов при решении математических задач студентами вузов спортивной направленности // Перспективы науки и образования. 2014. № 2 (8). С. 90-94.
- Потехина Е.В. Использование интернет-технологий при обучении студентов гуманитарных специальностей математическим дисциплинам: дис. … канд. пед. наук: 13.00.08. – Ставрополь, 2004. – 188 с.
- Валиханова О.А. Формирование информационно-математической компетентности студентов инженерных вузов в обучении математике с использованием комплекса прикладных задач / Автореферат диссертации на соискание ученой степени кандидата педагогических наук / Сибирский федеральный университет. Красноярск, 2008. – 23 с.
- Кузьмина А.В. Информационно-математическая компетентность студентов экономического профиля вузов. Вестник череповецкого государственного университета. 2011. Т. 2. № 3-32. С. 111-118.
- Лавина Т.А., Ющенко Н.С. Формирование информационно-математической компетентности у будущих специалистов социально-политологического профиля. Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. 2009. № 3-4. С. 50-54.
- BazhenovR.I., Luchaninov D.V. Use of blended learning elements for formation of a humanitarian student’s creative initiative at learning modern information technologies // Life Science Journal. 2014. Т. 11. № 11s. С. 371-374.
- Баженов Р.И. Проектирование методики обучения дисциплины «Информационные технологии в менеджменте» // Современная педагогика. 2014. № 8 [Электронный ресурс]. URL: http://pedagogika.snauka.ru/2014/08/2570 (дата обращения: 13.09.2014).
- Баженов Р.И. Проектирование методики обучения дисциплины «Интеллектуальные системы и технологии» // Современные научные исследования и инновации. 2014. № 5-2 (37). С. 48.
- Баженов Р.И. Организация научно-исследовательской работы студентов по дисциплине «Теория автоматов» // Современная педагогика. 2014. № 5 (18). С. 20.
- Баженов Р.И. О методике обучения проектированию информационных систем будущих менеджеров // Психология, социология и педагогика. 2014. № 8 [Электронный ресурс]. URL: http://psychology.snauka.ru/2014/08/3539 (дата обращения: 13.09.2014).
- Баженов Р.И. О методике преподавания дисциплины «Управление проектами информационных систем» // Современные научные исследования и инновации. 2014. № 3 (35). С. 55.
- Баженов Р.И. Об организации деловых игр в курсе «Управление проектами информационных систем» // Научный аспект. 2014. Т. 1. № 1. С. 101-102.
- Остапенко Р.И. Формирование математической компетентности студентов-психологов в условиях самодиагностики по курсу «Математические основы психологии» // Перспективы науки и образования, 2013. – № 6. – С. 91-96.
- Остапенко Р.И. Методические аспекты формирования информационно-математической компетентности студентов гуманитарных специальностей // Современные научные исследования и инновации. – 2013. – № 5 (25). – С. 29. URL: snauka.ru (дата обращения: 15.04.2014).
- Остапенко Р.И. Самодиагностика как условие формирования математической компетентности студентов психологических специальностей // Современные научные исследования и инновации. – 2013. – № 10 (30). – С. 44. URL: snauka.ru (дата обращения: 15.04.2014).
- Остапенко Р.И. Формирование информационно-математической компетентности студентов гуманитарных специальностей: методические аспекты // Перспективы науки и образования. 2013. № 4. С. 101-106.
- Остапенко Р.И. Структурное моделирование в науке и образовании: краткий обзор и перспективы развития // Современные научные исследования и инновации. – 2013. – № 9 (29). – С. 30. – URL: snauka.ru (дата обращения: 15.04.2014).
- Остапенко Р.И. Молодой специалист в сфере ИТ на рынке труда: представления и пожелания // Государственный советник. 2013. № 2. С. 82-86.
- Остапенко Р.И. Управление процессом формирования информационно-математической компетентности студентов вузов посредством самодиагностики // Государственный советник. 2014. № 1 (5). С. 160-164.
- Остапенко Р.И. О корректности применения количественных методов в психолого-педагогических исследованиях // Перспективы науки и образования. 2013. № 3. С. 63-67.
- Архандеева Л.В. Формирование математической компетентности студентов вузов спортивной направленности // Вектор науки ТГУ, 2010. – № 2(2). – С.17-20.
- Официальный сайт Федерации лыжных гонок России. URL: http://www.flgr.ru/ (дата обращения: 02.02.2014)