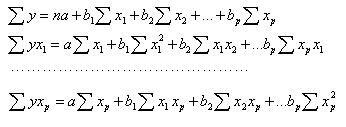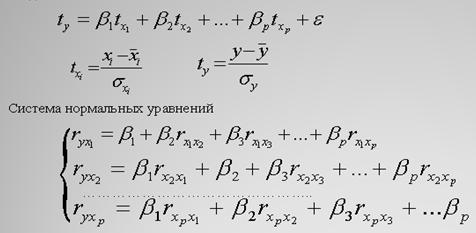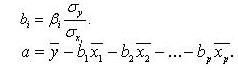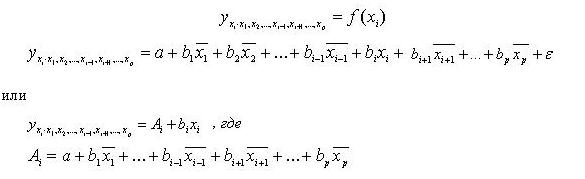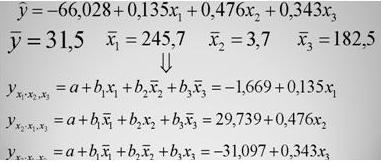Множественная регрессия позволяет строить модели с числом фактор-признаков влияния более одного, определяя при этом как их совокупное влияние на результатирующий признак, так и влияние каждого из них в отдельности.
Спецификация моделей множественной регрессии заключается в отборе фактор-признаков и выборе уравнения регрессии.
Требования к включаемым в модель факторам:
◦ Они должны быть количественно измеримы
◦ Они не должны находиться в корреляционной зависимости
Пример 1. На основе статистических данных построена модель зависимости себестоимости единицы выпускаемой продукции (у) от производительности труда (z) и заработной платы работников (х):
Анализ данной модели показывает, что при увеличении фактора заработной платы на 1 усл.ед., себестоимость увеличится на 5 усл.ед., если же увеличится производительность труда на 1 усл.ед, то себестоимость будет уменьшена на 10 усл.ед.
Вычисленный коэффициент парной корреляции ![]() свидетельствует о сильной межфакторной взаимосвязи или коллинеарности (т.е. факторы помимо влияний на результативный признак, оказывают еще и сильное влияние друг на друга), т.е. включение их в модель нецелесообразно. В данном случае используется принцип исключения факторов:
свидетельствует о сильной межфакторной взаимосвязи или коллинеарности (т.е. факторы помимо влияний на результативный признак, оказывают еще и сильное влияние друг на друга), т.е. включение их в модель нецелесообразно. В данном случае используется принцип исключения факторов:
◦ если факторы коллинеарны , то один из них исключается
◦ в модель регрессии добавляется фактор, имеющий наименьшую тесноту связи с другими рассматриваемыми факторами
В модели множественной регрессии также может присутствовать мультиколлинеарность факторов, т.е. более двух факторов оказываются связанными между собой линейной зависимостью. В этом случае выполняется проверка нулевой гипотезы H0: ![]() где R – матрица коэффициентов корреляции. При этом чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
где R – матрица коэффициентов корреляции. При этом чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
На втором этапе спецификации модели регрессии осуществляется выбор ее одели. При этом наиболее часто используемые функциональные зависимости имеют вид:
Рисунок 1 – Виды моделей множественной регрессии
Вычисление параметров выбранного уравнения множественной регрессии может осуществляться методом наименьших квадратов (МНК) для уравнения в обычном масштабе (решение системы нормальных уравнений) или методом наименьших квадратов (МНК) для стандартизованного уравнения.
Так для определения параметром линейной модели множественной регрессии метод наименьших квадратов сводится к решению системы нормальных уравнений:
Метод наименьших квадратов (МНК) для стандартизованного уравнения имеет
вид:
Рисунок 2 – МНК для стандартизированного уравнения
Переход от стандартизованного уравнения к обычному осуществляется следующим образом:
При этом достоинство стандартизованных уравнений заключается в том, что возможно исключение из модели факторов с наименьшим значением ![]()
Помимо стандартизированных уравнений возможно рассмотрение частных уравнений регрессии, которые связывают результативный признак с фактором xi при условии, что остальные экзогенные переменные (факторы) остаются неизменными на среднем уровне:
Пример 2.
Имеется модель влияния на величину импорта y на определенный товар следующих факторов: объем отечественного производства x1, изменения запасов x2 и потребление на внутреннем рынке х3:
Рисунок 3 – Частные уравнения регрессии
Таким образом, множественная регрессия является продуктивным методом исследования статистических данных.
Библиографический список
- Сухих Е.С., Зеленина Л.И. Эконометрическое моделирование как эффективный метод анализа в научных исследованиях студентов // Современная педагогика. 2014. № 12 [Электронный ресурс]. URL: http://pedagogika.snauka.ru/2014/12/3116 (дата обращения: 17.12.2014).
- Федькушова С.И., Зеленина Л.И. Математические методы обработки данных в научно-исследовательских работах студентов // Современная педагогика. 2015. № 1 [Электронный ресурс]. URL: http://pedagogika.snauka.ru/2015/01/2894 (дата обращения: 07.01.2015).
- Федькушова С.И., Зеленина Л.И. Корреляционный анализ в исследовании функционально-технологических свойств смесей// Вестник магистратуры. 2014. № 11-1 (38). С. 53-56.
- Федькушова С.И., Зеленина Л.И. Моделирование на основе нечеткого регрессионно-факторного анализа // Проблемы современной науки и образования /Problems of modern science and education/ 2014. № 8 (26). С.32-34