Вычислительный эксперимент является одним из эффективных методов познания, который широко используется в современной науке, наряду с наблюдением, экспериментальным изучением, математическим моделированием и т.д. Вычислительный эксперимент фактически является экспериментом над компьютерной моделью исследуемого объекта [1, 2], и в ряде случаев имеет преимущества над другими методами исследования. Не все задачи можно решить аналитическими методами, не все явления и процессы можно изучить экспериментально. Метод компьютерного моделирования позволяет выявить основные факторы, определяющие свойства изучаемых объектов, исследовать отклик физической системы на изменения ее параметров, начальных условий и внешних воздействий [5, 6].
Проблема использования вычислительного эксперимента при изучении физики остается актуальной. Компьютерные модели позволяют взглянуть на изучаемое явление в другом пространственно–временном масштабе, получить полную информацию об изменяющихся физических величинах, построить соответствующие графики и траектории, в динамике “пронаблюдать” исследуемые процессы, сформировать у учащихся наглядный образ изучаемого явления, проникнуть в его физическую сущность, получить ответы на вопросы, которые остаются открытыми после проведения реального эксперимента.
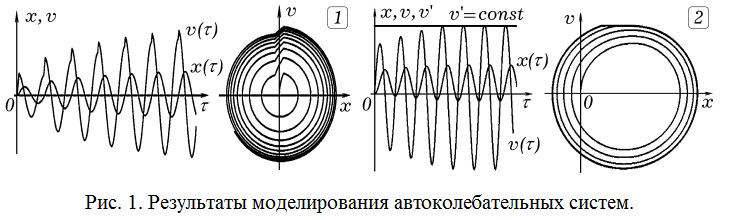
Рассмотрим, например, изучение механических автоколебаний. Аналитическое решение дифференциального уравнения слишком громоздко. Компьютерная модель позволяет исследовать автоколебания физического маятника часов с гирей (рис. 1.1) или маятника Фроуда (рис. 1.2) при различных параметрах системы [3]. Выполнив учебный эксперимент, можно убедиться в правильности математической и компьютерной моделей, подтвердить теорию этого явления.
Допустим, учитель рассказывает о строении Солнечной системы. Как сформировать у школьника ее наглядный образ? Как показать движение планет вокруг Солнца и их взаимодействие друг с другом? Обычные рисунки статичны, учащихся больше заинтересует подвижная картинка, получающаяся как результат компьютерного моделирования (рис.2). В тот момент, когда они видят происходящее на экране монитора движение светящейся точки вокруг центра, в сознании формируется наглядный образ вращения планеты вокруг Солнца [4]. Важно понимать, что речь идет не о какой–нибудь анимации: движение планет рассчитывается по законам Ньютона. Чтобы понять решение этой задачи, достаточно школьной физики. Учитель обращает внимание на то, что вблизи Солнца планета увеличивает свою скорость, а при удалении от него –– уменьшает. Изменяя массу планеты, начальные координаты и скорость, можно исследовать влияние этих величин на ее движение.
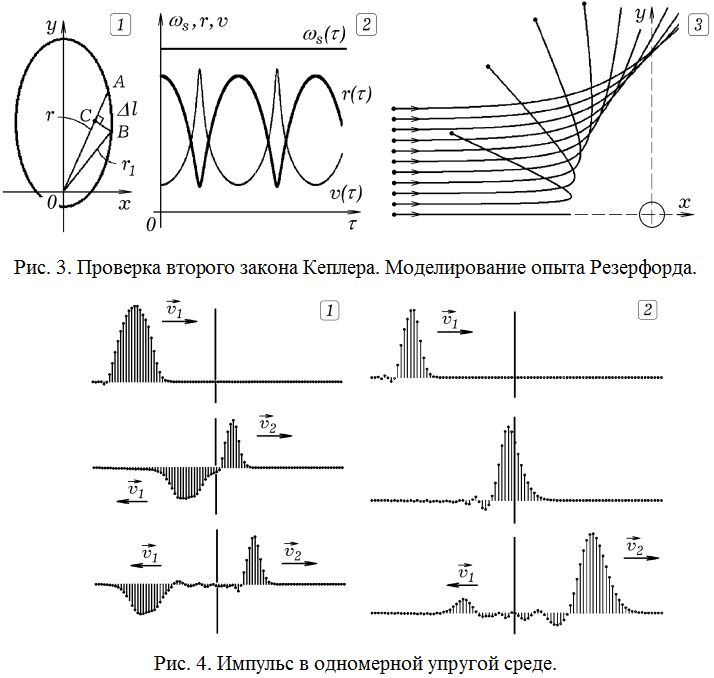
Как доказать второй закон Кеплера на уроке физики? Как исследовать движение альфа–частиц в поле ядра атома золота (опыт Резерфорда)? Анализ перечисленных вопросов на качественном уровне не является убедительным доказательством. На помощь приходит компьютерная модель движения точки в поле центральных сил (рис. 3). Промоделировав движение планеты вокруг Солнца, можно рассчитать ее секториальную скорость и убедиться в том, что она остается постоянной (рис. 3.1 и 3.2). Изменяя прицельный параметр и скорость альфа–частиц, школьники могут провести серию вычислительных экспериментов (рис. 3.3), определив их влияние на траекторию движения. Аналитическое решение этих задач выходит за пределы школьной программы.
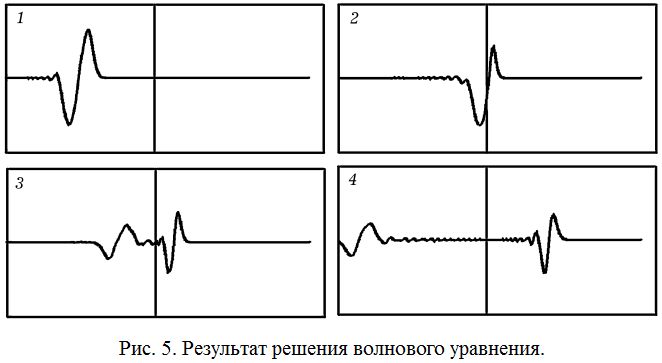
Учащиеся могут заниматься учебно–исследовательской работой, выполняя при этом реальные и вычислительные эксперименты. Допустим, они изучают явление отражения импульса от границы раздела двух сред. Можно создать компьютерную программу, моделирующую одномерную среду (струну), упругие и инертные свойства которой, начиная с середины, изменяются скачком. Если вызвать колебания крайнего левого элемента, то по среде побежит волна (импульс), которая, дойдя до середины, частично отразится в первую среду, а частично пройдет во вторую среду (рис. 4). Это же явление может быть исследовано с помощью программы, решающей волновое уравнение для одномерной среды (рис. 5). Обсуждаемые компьютерные модели [3, 4] дополняют реальные эксперименты, проводимые учителем со школьниками.
Определенный интерес для школьников, освоивших программирование, представляет собой компьютерная модель автоволновых процессов, в которой активная среда промоделирована системой клеточных автоматов, работающих по определенной программе. На рис. 6 показан результат моделирования дифракции автоволн на препятствии. Учащиеся в динамике наблюдают процесс распространения автоволны, образование однорукавных и двурукавных автоволн, при этом у них формируется наглядных образ рассматриваемых явлений. Компьютерная модель позволяет провести серию вычислительных экспериментов при различных параметрах среды [3, 4].
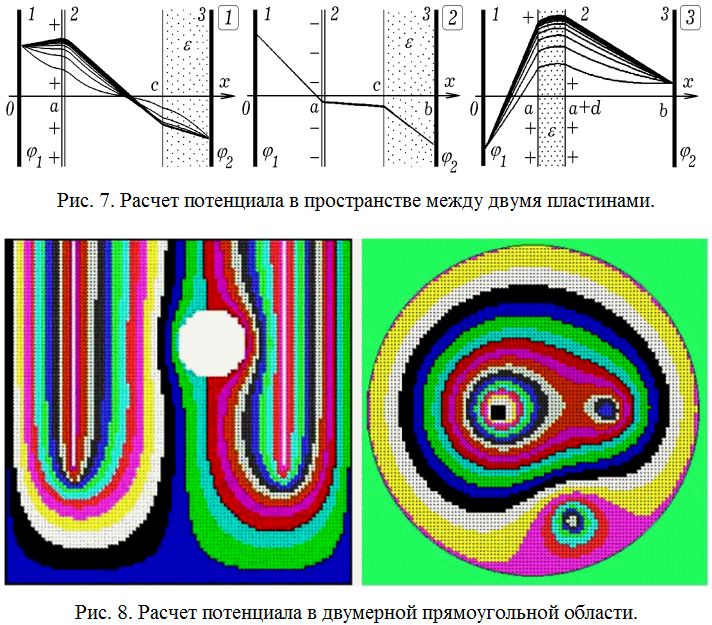
В классах с углубленным изучением дисциплин физико–математического цикла имеет смысл познакомить учащихся с методами расчета электрических полей. На рис. 7 и 8 представлены результаты решения этой задачи в одномерном и двумерном случаях при различных граничных условиях и заданных распределениях плотности заряда [3, 4].
Учащимся, интересующимся физикой и информатикой, можно показать компьютерную модель течения жидкости (рис. 9). Части жидкости, имеющие различные скорости, окрашиваются в разные цвета, что позволяет создать у учащихся наглядный образ изучаемого явления, сформировать представления о вычислительных методах решения задач гидродинамики [3, 4].
При изучении интерференции возникает необходимость показать учащимся интерференционную картину, возникающую при наложении двух когерентных волн. Компьютерная модель не заменяет реальный опыт, но может служить его дополнением. Получающиеся распределения интенсивности при различных частотах источников показаны на рис. 10. Изменяя расстояние между источниками, их частоту и фазу, учащиеся могут исследовать влияние этих факторов на результат интерференции. Понятно, что в реальном эксперименте визуализировать интерференционную картину не так просто.
Таким образом, использование компьютерных моделей при изучении физических явлений помогает: 1) сформировать у учащихся наглядный образ изучаемого явления; 2) исследовать динамику развития явления в другом пространственно–временном масштабе при различных параметрах системы, начальных условиях и внешних воздействиях; 3) повысить интерес учащихся к физике и информатике. Все это позволяет утверждать, что компьютерные модели и учебный вычислительный эксперимент дополняют теоретическое и экспериментальное изучение физических явлений [1–6].
Библиографический список
- Гулд, Х. Тобочник Я. Компьютерное моделирование в физике: В 2 ч. / Х. Гулд, Я. Тобочник. –– М.: Мир, 1990. –– Ч. 2. –– 400 с.
- Кунин С. Вычислительная физика. –– М.: Мир, 1992. –– 518 с.
- Майер Р.В. Задачи алгоритмы программы: Электронное пособие // Номер госрегистрации –– 0321203016. Режим доступа: URL: http://maier-rv.glazov.net
- Майер Р.В. Компьютерное моделирование физических явлений. –– Глазов: ГГПИ, 2009. –– 112 с. (http://maier-rv.glazov.net)
- Федоренко, Р. П. Введение в вычислительную физику. Учебное пособие для вузов / Р.П.Федоренко. – М.: Изд–во Моск. физ.–техн. Ин–та,1994. –528 с.
- Woolfson M.M., Pert G.J. An Introduction to Computer Simulation. –– Oxford University Press, 1999. –– 311 p.