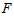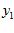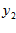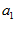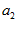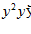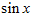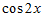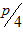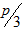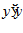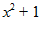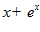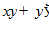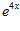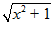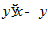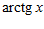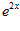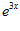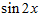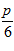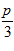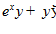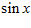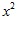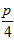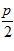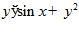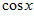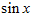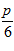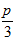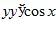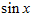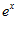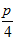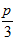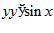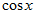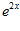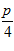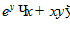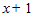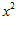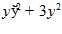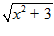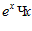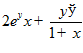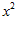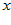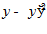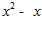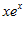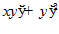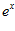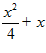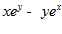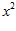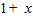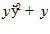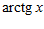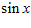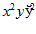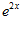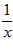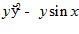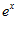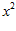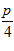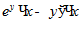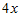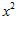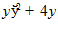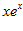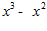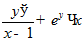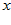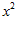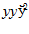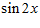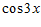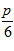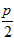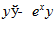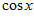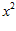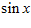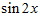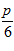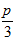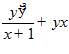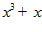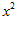1. ПРОСТЕЙШАЯ ЗАДАЧА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
Дан функционал J[y]=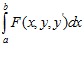 (1)
(1)
при граничных условиях у (а )= у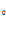 , у (в) = у
, у (в) = у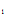 (2)
(2)
Задача отыскания экстремума этого функционала называется простейшей задачей вариационного исчисления. Основой для решения задачи является утверждение: Если функция у(х) дает экстремум (1) то она является решением уравнения Эйлера
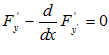
Решение уравнения Эйлера – это семейство кривых у = у (х, С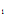 ,С
,С ) которые называются экстремалями функционала (1). Константы С
) которые называются экстремалями функционала (1). Константы С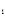 и С
и С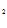 находятся из граничных условий (2).
находятся из граничных условий (2).

Пример 1. 
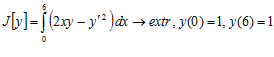 .
.
□ 
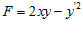
(Рассматриваем 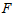 как функцию трех переменных x, y, y
как функцию трех переменных x, y, y ).
).
а)
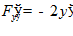 ;
;
б) 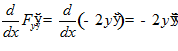 ;
;
в)
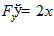 .
.
Составляем уравнение Эйлера
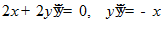 . Интегрируем дважды:
. Интегрируем дважды:

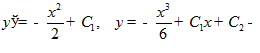 экстремали (множество кривых).
экстремали (множество кривых).
Используя краевые условия, находим
1 = C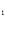 , 1= -216/6 +6 C
, 1= -216/6 +6 C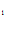 + C
+ C
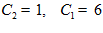 .
.
Единственная экстремаль 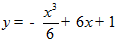

Пример 2.
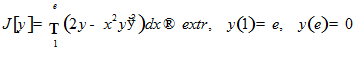
□ Уравнение Эйлера 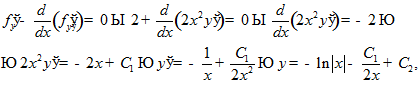

или, с учетом 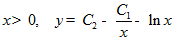 .
.
Используем краевые условия:
e = C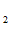 - C
- C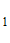 , 0= C
, 0= C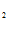 – C
– C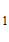 /e -1, откуда C
/e -1, откуда C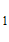 =-е, C
=-е, C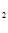 =0.
=0.
Единственная экстремаль 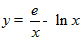 .■
.■
2. ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ.
1. Дан функционал вида
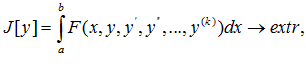
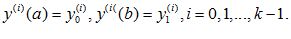
Если функция у(х) дает экстремум данному функционалу , то она является решением уравнения Эйлера-Пуассона
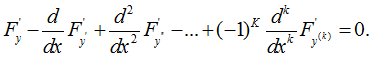
Пример 3. 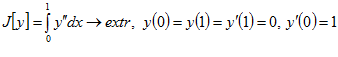 .
.
□ . Уравнение Эйлера-Пуассона,
. Уравнение Эйлера-Пуассона, 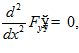 т.е.
т.е. 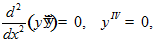 отсюда
отсюда 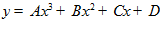 ,
, 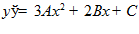 .
.
Для нахождения коэффициентов используем граничные условия:
D = 0,
A + B + C + D = 0, откуда A = 1, B = – 2, C= 1, D = 0.
3A + 2B + C= 0,
C = 1.
Получаем единственную экстремаль
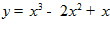 .
.
Пример 4.
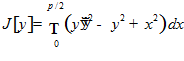
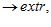
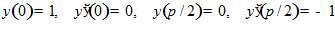 .
.
□ 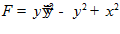 .
.
Уравнение Эйлера-Пуассона: 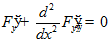 ,
,
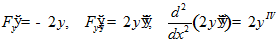 ,
,
так что уравнение имеет вид 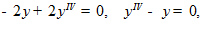
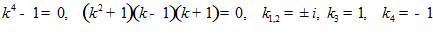 ,
,
y=C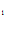 COSX + C
COSX + C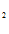 SINX + C
SINX + C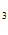 e
e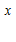 + C
+ C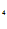 e
e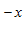
y = – C
= – C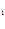 SINX + C
SINX + C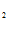 COSX + C
COSX + C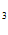 e
e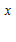 – C
– C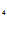 e
e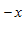
Используем граничные условия:
C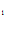 +C
+C +C
+C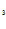 =1,
=1,
C +C
+C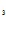 - C
- C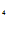 = 0, из системы C==1, C
= 0, из системы C==1, C =0, C
=0, C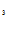 =0, C
=0, C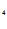 =0.
=0.
C +C
+C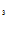 e
e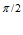 +C
+C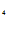 e
e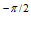 =0,
=0,
-C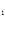 +C
+C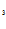 e
e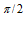 -C
-C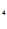 e
e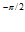 =-1.
=-1.
Единственная экстремаль 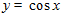 . ■
. ■
2. Дан функционал вида
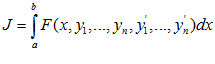
Граничные условия 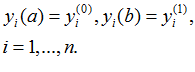
Экстремали находим из системы уравнений Эйлера
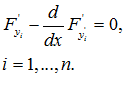
Пример 5. 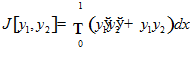
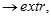
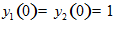 ,
, 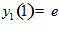 ,
, 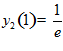 .
.
□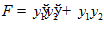 ,
, 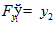 ,
, 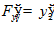 ,
, 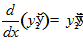 ,
,
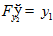 ,
, 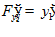 ,
, 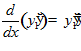 .
.
Система уравнений Эйлера имеет вид: y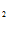 – y
– y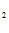
 =0,
=0,
y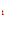 – y
– y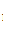
 = 0.
= 0.
Рассмотрим второе уравнение 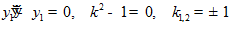 , отсюда
, отсюда 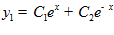 , аналогично
, аналогично 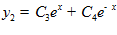 .
.
Для определения констант используем граничные условия
C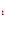 +C
+C =1 откуда
=1 откуда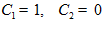 .
.
C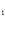 e+ C
e+ C /e = e
/e = e
C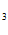 +C
+C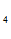 =1, C
=1, C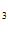 + C
+ C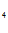 /e = 1/e
/e = 1/e
откуда 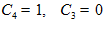 .
.
Получаем 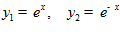 . ■
. ■
Задачи для самостоятельного решения
1. 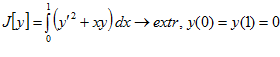 .
.
2. 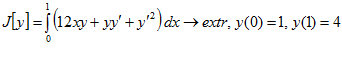 .
.
3. 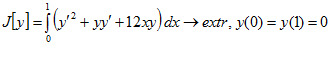 .
.
4. 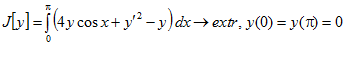 .
.
5. 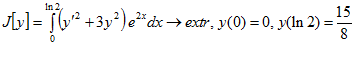 .
.
6. 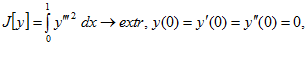
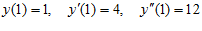 .
.
7. 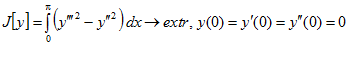 ,
,
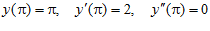 .
.
8. 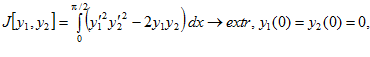
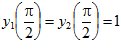 .
.
9. 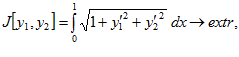
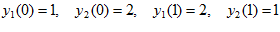 .
.
ЗАДАНИЕ 1
а) Вычислить функционал 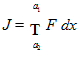 для заданных функций
для заданных функций  и
и  .
.
б) Написать уравнение Эйлера для функций 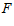 (Таблица 1).
(Таблица 1).
Таблица 1- Исходные значения.
| N |
|
|
|
|
|
| 1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
|
|
|
|
|
| 2 |
|
|
|
0 |
2 |
| 3 |
|
|
|
1 |
2 |
| 4 |
|
|
|
1 |
2 |
| 5 | 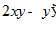 |
|
|
|
|
| 6 |
|
|
|
|
|
| 7 |
|
|
|
|
|
| 8 |
|
|
|
|
|
| 9 |
|
|
|
0 |
|
| 10 |
|
|
|
1 |
2 |
| 11 |
|
|
|
1 |
2 |
| 12 |
|
|
|
1 |
2 |
| 13 |
|
|
|
0 |
1 |
| 14 |
|
|
|
0 |
1 |
| 15 |
|
|
|
1 |
2 |
| 16 |
|
|
|
0 |
1 |
| 17 |
|
|
|
1 |
2 |
| 18 |
|
|
|
0 |
|
| 19 |
|
|
|
1 |
2 |
| 20 |
|
|
|
1 |
2 |
| 21 |
|
|
|
1 |
2 |
| 22 |
|
|
|
|
|
| 23 |
|
|
|
1 |
2 |
| 24 |
|
|
|
|
|
| 25 |
|
|
|
0 |
1 |
ЗАДАНИЕ 2
Найти экстремали функционала
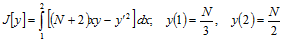 ,
,
где 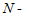 номер по списку.
номер по списку.
ЗАДАНИЕ 3
Найти экстремали функционала
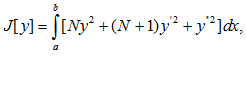
N – Номер по списку.
3. ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
Найти 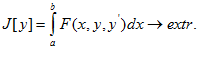
Решение: К уравнению Эйлера добавляют естественные краевые условия
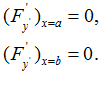
Замечание: Если один конец закреплен, например у(а) = с , – то естественное краевое условие записывают для другого конца 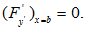
Пример 6.
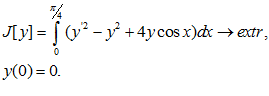
Решение: Уравнение Эйлера
-2y + 4 соsx – 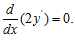
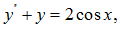
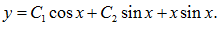
Найдем производную
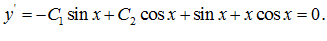
На правом конце
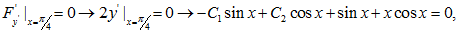
В точке =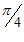
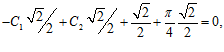 из данного равенства и используя граничные условия у(0)=0 ,
из данного равенства и используя граничные условия у(0)=0 , 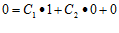 определяем
определяем
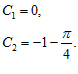
Экстремаль 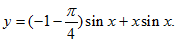
4. ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ
Найти 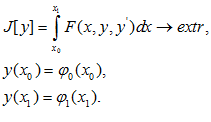
Решение:
1. Из уравнения Эйлера 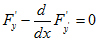 находим
находим
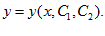
2. Запишем условия трансверсальности (условия, что концы кривой лежат на заданных кривых).
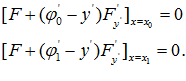
Добавляя уравнения связи
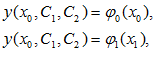
решаем совместно, определяем 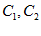 и концы
и концы 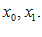
Замечание: Если заданы обычные граничные условия для одного конца,
то условия трансверсальности записывается только для другого конца кривой.
Примеры 7.
Пример 1. 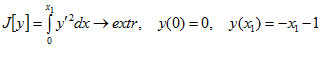 .
.
□ 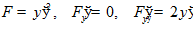
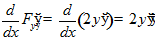 .
.
Уравнение Эйлера 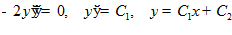 .
.
Условие трансверсальности
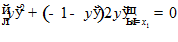 т.к.
т.к. 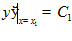 то
то
C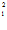 + (-1- C
+ (-1- C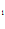 ) 2 C
) 2 C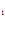 = 0,
= 0,
C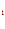 0 +C
0 +C =0,
=0,
C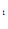 x
x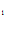 + C
+ C = – x
= – x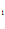 – 1.
– 1.
Их системы находим C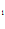 = -2 , C
= -2 , C =0, x
=0, x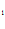 = 1.
= 1.
Ответ:
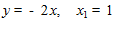 . ■
. ■
Пример 8. 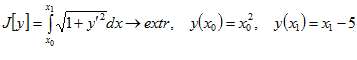 .
.
□ 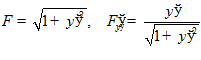 .
.
Уравнение Эйлера 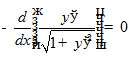 , тогда
, тогда 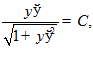
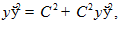
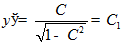 ,
,
тогда  .
.
Условия трансверсальности совместно с уравнениями связи, учитывая, что 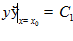 и
и 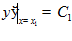 :
:

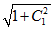 + (2x
+ (2x – C
– C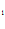 )C
)C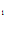 /
/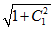 =0,
=0,
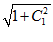 +1(1- C
+1(1- C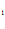 ) C
) C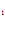 /
/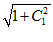 =0,
=0,
C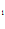 x
x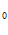 +C
+C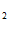 = x
= x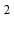
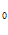 ,
,
C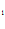 x
x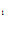 + C
+ C = x
= x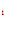 – 5.
– 5.
Решаем совместно и получаем
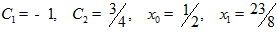 .
.
Ответ: 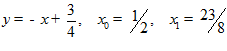 .■
.■
Пример 9. Найти экстремали функционала
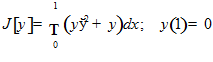 .
.
□ 1. Уравнение Эйлера 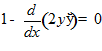 ,
,
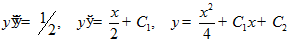 .
.
-
Естественное краевое условие в точке
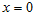
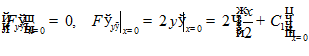 .
.
Получаем систему
2(0/2 +C
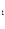 ) = 0,
) = 0,
1/4 + C
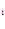 1 + C
1 + C = 0.
= 0.
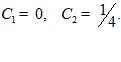
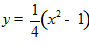 . ■
. ■
Задачи для самостоятельного решения
1.
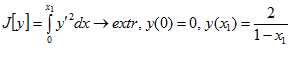 .
.
2.
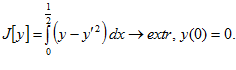
3.
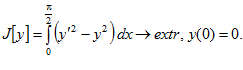
4.
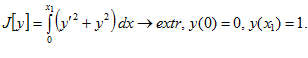
5.
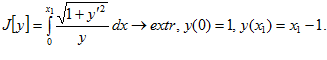
6.
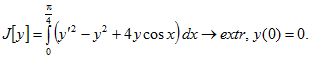
7.
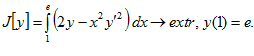
8.
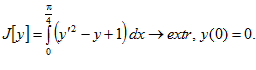
9.
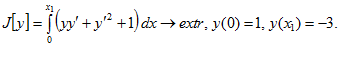
10.
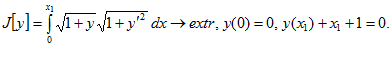
ЗАДАНИЕ 4
Дано: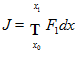 и
и 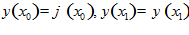 .
.
Найти экстремаль
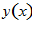 и концы отрезка
и концы отрезка 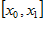 , (если
, (если 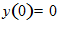 , тогда
, тогда 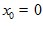 ).
).
ЗАДАНИЕ 5
Дано:
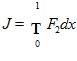 и
и 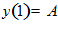 . Найти экстремаль
. Найти экстремаль 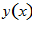 (Таблица 2).
(Таблица 2).
Таблица 2- Исходные данные для задания 4 и 5
N 
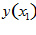
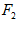
А
1 2
3
4
5
6
1. 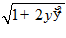
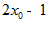
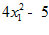
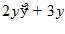
4
2. 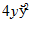
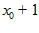
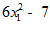
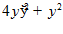
5
3. 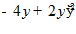
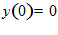
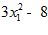
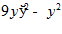
1
4. 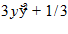
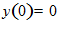
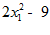
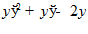
3
5. 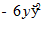
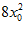
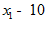
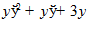
5
6. 
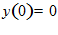
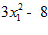
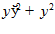
1
7. 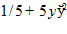
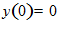
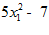
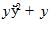
0
8. 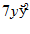
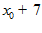
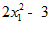
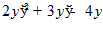
4
9. 
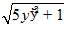
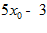
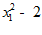
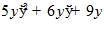
6
10. 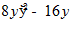
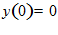
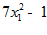
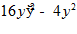
1
11. 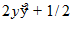
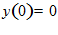
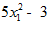
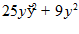
2
12. 
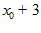
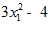
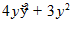
3
13. 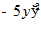
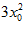
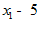
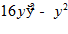
7
1 2
3
4
5
6
14. 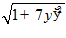
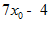
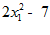
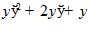
2
15. 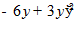
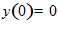
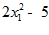
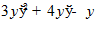
3
16. 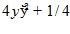
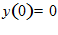

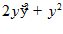
6
17. 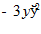
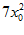
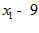
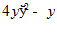
8
18. 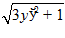
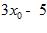
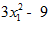
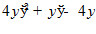
9
19. 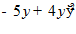
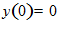
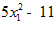
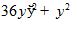
3
20. 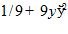
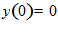
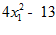
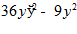
5
21. 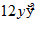
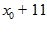

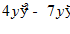
2
22. 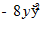
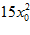
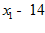
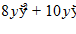
7
23. 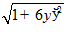
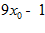
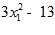
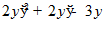
5
24. 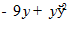
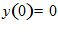
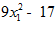
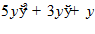
7
25. 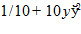
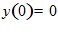
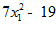
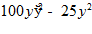
3
Библиографический список
-
Ванько В.И., Ермошина О.В., Кувыркин Г.Н. Вариационное исчисление и оптимальное управление. – М.: Издательство МГТУ им. Н.Э. Баумана, 1999. – 488 с.
-
Гельфанд И.М., Фомин С.В. Вариационное исчисление. – М.: Физматгиз, 1984. – 228 с.
-
Краснов М. Л., Макаренко Г. И., Киселёв А.И. Вариационное исчисление(задачи и упражнения). – М.: Наука, 1984. – 191 с.
-
Данко П.Е. Высшая математика в упражнениях и задачах в 2 т. – М.: Высшая школа, 1986. – т. 2. – 414 с.
-
Вуколов Э.А. и др. Сборник задач по математике для втузов. – М.: Наука, 1984. – 606 с.